Chapitre 7
La structure des coûts, le volume et la capacité

Objectifs

 Après avoir étudié ce chapitre, vous serez capable :

Analyser les décisions influant sur la structure des coûts

Nous présentons l’analyse coût-volume-bénéfice (CVB) pour étudier cette importante catégorie de décisions. Nous définissons aussi les concepts de point mort, de marge de sécurité, de seuil d’indifférence et de bénéfice potentiel qui y sont associés. L’analyse CVB se révèle particulièrement utile pour établir l’effet de différents scénarios de volume d’activité mais également de structures de coûts sur le bénéfice.

Calculer, à l’aide de l’analyse CVB, le point mort, la marge de sécurité et le bénéfice potentiel dans une situation donnée.

La compréhension de ces trois paramètres passe par la maîtrise totale du calcul de ceux-ci.

Établir le seuil d’indifférence entre deux propositions affectant la structure des coûts d’une entreprise

Le seuil d’indifférence, souvent exprimé selon le volume d’activité, est un point de repère intéressant pour évaluer deux propositions, car il indique à quel volume l’une devient plus intéressante que l’autre.

Étudier l’effet de la capacité utilisée sur le bénéfice

Cet objectif s’insère dans la problématique de plusieurs chapitres de cette première partie, soit celle du traitement et de l’interprétation des coûts indirects.

Questions de révision

1. La structure des coûts définit la proportion de coûts fixes et de coûts variables engagés par une entreprise pour la production de biens ou la prestation de services.

2. Le volume d’extrants est le volume de biens et de services produit par une entreprise; on dit également volume d’activité.

3. La combinaison d’extrants décrit une proportion relative de produits et de services issus d’une entreprise.

4. L’analyse coût-volume-bénéfice (CVB) vise à évaluer l’effet sur le rendement financier de l’entreprise :

 5. Les paramètres du modèle CVB sont : le volume, le revenu et le coût total, le coût fixe et la marge sur coûts variables unitaire.

6. Le point mort correspond au volume d’activité auquel l’entreprise a des revenus et des coûts égaux.

7. La marge de sécurité exprime la différence entre le volume d’activité atteint, ou que l’on prévoit atteindre, et le volume d’activité correspondant au point mort.

8. Elle indique la diminution du volume d’activité que l’entreprise pourrait absorber sans subir de perte.

9. Le bénéfice potentiel représente le bénéfice maximal que vise l’entreprise lorsqu’elle fonctionne à pleine capacité.

10. Le seuil d’indifférence indique le volume d’activité auquel deux propositions portant sur la structure des coûts produisent le même résultat net. Il intervient pour éclairer le choix entre deux propositions; il fournit un point de repère en fonction du volume à partir duquel l’une des deux propositions devient avantageuse pour l’entreprise.

11. On peut généraliser l’analyse CVB en utilisant une unité équivalente pour mesurer le volume.

12. Le projet d’investissement a souvent pour effet de modifier la structure des coûts de l’entreprise; le modèle CVB indique alors le volume de production qui rendra le projet avantageux.

13. Il est souhaitable de le faire lorsqu’on doit analyser simultanément plusieurs facteurs décrivant et expliquant la variabilité des produits.

14. La capacité se mesure en fonction du volume maximal d’extrants qu’il est possible de produire dans un cadre donné.

15. La capacité théorique correspond au volume maximal d’extrants qu’une entité peut produire en fonction de l’hypothèse théorique, irréalisable, selon laquelle il n’y a aucun arrêt de production, aucun gaspillage, aucun entretien; la capacité pratique se réfère à des conditions normales d’exploitation; la capacité normale concerne une moyenne de capacité à long terme; la capacité prévue correspond à celle que l’on pense utiliser dans l’année.

16. La capacité productive englobe les ressources directement engagées dans la fabrication d’un produit ou la prestation d’un service.

 Exercices

Exercice 7.1 Évaluation du bénéfice, du point mort et de la marge de sécurité

1. L’équation de la droite des revenus est : Revenus = 255 $ ´ Nombre d’unités vendues  On peut vérifier, à l’aide des données de l’exercice, que le prix moyen est :
255 = Revenus/nombre d’unités vendues.
L’équation de la droite des coûts est :
Coûts = 3 959 657 $ + 71,6129 $ ´ Nombre d’unités vendues.

2. Le point mort x0 correspond au nombre d’unités tel que Revenus = Coûts, c’est-à-dire: 255 $ ´ x0 =3 959 657 $ + 71,6129 $ ´ x0
Donc, x0 = 3 959 657 $/(255 $ – 71,6129 $) = 21 592 unités.

3. L’entreprise prévoit réaliser le mois prochain :
Résultat net = (255 $ – 71,6129 $) ´ 25 000 – 3 959 657 $ = 625 021 $.

4. La marge de sécurité est de 3 408, soit 25 000 – 21 592.

Exercice 7.2 Modification de la structure de coûts

1. Il faut d’abord établir l’équation donnant le résultat net. Les ventes sont de 15 000 unités par mois pour un montant de 1 050 000 $, donc le prix de vente est de 70 $/unité.
Les coûts totaux sont de 900 000 $ puisque le bénéfice est de 150 000 $ sur des ventes de
1 050 000 $. Étant donné que 50 % des coûts sont fixes, il y a 450 000 $ de coûts fixes et
450 000 $ de coûts variables, soit 30 $/unité.

L’équation donnant le résultat net est donc la suivante :
Résultat net = (70 $ - 30 $) ´ Nombre d’unités vendues – 450 000 $.

Le point mort actuel est x0 tel que :
0 $ ´ x0 = 450 000 $, c’est-à-dire x0 = 11 250 unités.

L’équation donnant le résultat net, dans le cas où le projet serait mis en œuvre, est la suivante : Résultat net = (70 $ - 15 $) ´ Nombre d’unités vendues – 675 000 $.

Le point mort actuel est x0 tel que :
55 $ ´ x0 = 675 000 $, c’est-à-dire x0 = 12 273 unités.

L’effet du projet sur le point mort est donc de le faire passer de 11 250 à 12 273 unités, soit un accroissement de 1 023 unités.
 

2. Le seuil d’indifférence associé au projet correspond au volume d’activité où le projet génère le même bénéfice que celui de la situation actuelle, c’est-à-dire le volume x tel que :
40 $ ´ x - 450 000 $ = 55 $ ´ x - 675 000 $,
x = (675 000 $ – 450 000 $)/(55 $ - 40 $)
x = 15 000 unités
 

3. La marge de sécurité passe de 3 750 unités à 2 727 unités, soit une diminution de 1 023 unités, laquelle correspond à l’augmentation du point mort.

  Exercice 7.3 Évolution de la combinaison de produits
 

1. Le point mort actuel est le nombre d’unités x0 tel que le résultat net soit nul, c’est-à-dire:
30,80 $ ´ x0 = 1 500 000 $, soit x0 = 48 701 unités.
La moyenne de 30,80 $ vient de la marge sur coûts variables totale, 1 540 000 $, divisée par le nombre total d’unités vendues, soit 50 000 comme le démontre le tableau qui suit :


 

2. Selon le premier expert, la marge sur coûts variables par unité devient 44,50 $, soit la marge sur coûts variables totale, 2 670 000 $, divisée par le nombre total d’unités vendues, soit 60 000.
Selon le deuxième expert, la marge sur coûts variables par unité devient 31,00 $, soit la marge sur coûts variables totale, 1 860 000 $, divisée par le nombre total d’unités vendues, soit 60 000.
 

3. Oui, l’entreprise devrait baisser son prix unitaire de 40 $, car cela lui permettrait d’augmenter son résultat net de 1 120 000 $. En effet, la marge sur coûts variables de la gamme de produits G5 passerait de 320 000 $, soit 2 000 unités à 160 $, à 1 440 000 $, soit 12 000 unités à
120 $.

Exercice 7.4 Généralisation de l’analyse CVB

1. Le tableau qui suit présente le calcul de la marge horaire sur coûts variables de chacun des cinq produits de l’échantillon.

2. Le point mort de l’usine est de 175 000 heures, soit 3 500 000 $/20 $ l’heure.

3. L’automatisation n’a aucun effet sur le prix de vente moyen qui demeure à 44 $ l’heure. Par contre, le coût variable moyen à l’heure diminue de moitié, passant de 24 $ l’heure à 12 $ l’heure de sorte que la marge horaire sur coûts variables passe de 20 $ l’heure à 32 $ l’heure. Les coûts fixes grimpent à 5 300 000 $. L’équation suivante résume le calcul du nouveau point mort :
32 $ l’heure ´ x0 = 5 300 000 $, soit x0 = 165 625 heures.

4. Le seuil d’indifférence associé à ce projet est de 150 000 heures. On l’obtient en cherchant le volume, c’est-à-dire le nombre d’heures dans ce problème, pour lequel le résultat net selon la situation actuelle est égal au résultat net selon le projet d’automatisation d’une partie de l’usine. L’équation qui suit permet de trouver ce volume :
20 $ ´ x - 3 500 000 $ = 32 $ ´ x - 5 300 000 $,
x = (5 300 000 $ – 3 500 000 $)/(32 $ - 20 $)
x = 150 000 heures.

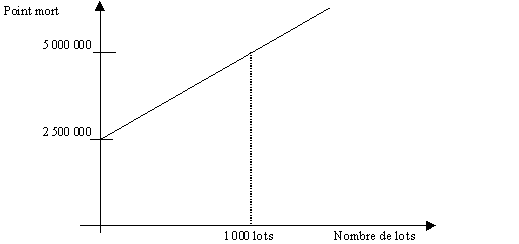
Exercice 7.5 Analyse d’un point mort variable

1. Il faut d’abord calculer les ventes au point mort. Or, la marge sur coûts variables par unité est de 20 $, soit 25 $ - 5 $; les frais fixes sont égaux à 50 000 000 $ + 800 lots ´ 50 000 $/lot, soit 90 000 000 $. Donc le point mort est le volume x0 tel que :
20 $ ´ x0 = 90 000 000 $, soit x0 = 4 500 000 unités.
Les ventes au point mort sont de 112 500 000 $, soit 4 500 000 unités ´ 25 $/unité. La marge de sécurité est donc de 37 500 000 $ (ou de 1 500 000 unités),
soit 150 000 000 $ - 112 500 000 $.

2. Le tableau qui suit résume le calcul du point mort dans le cas où l’entreprise mettrait en fabrication un nombre de lots différents :

3. Le graphique du point mort en fonction du nombre de lots.
La pente de la droite est de 2 500 $ par lot, soit 50 000 $/20 $.


 

Exercice 7.6 Points morts spécifiques et point mort global

  1. Le tableau qui suit présente les points morts spécifiques de chacune des familles de produits.

    2. Le tableau qui suit est utile pour calculer la marge par heure : 


     
     

  2. Le tableau qui suit indique le calcul du point mort global de l’entreprise.

Si vous faites les calculs manuellement et que vous vous utilisiez le montant arrondi des marges soit respectivement 10,42 $ et 15,98 $, vous obtiendrez 634 578 et 413 786.

La marge sur coûts variables de 10,42 $ a été obtenue en divisant la somme des marges sur coûts variables des 5 familles de produits par le nombre total d’unités des 5 familles de produits. De même, la marge sur coûts variables par heure a été obtenue en divisant la somme des marges sur coûts variables par heure par le nombre total d’heures consacrées à tous les produits.

Exercice 7.7 Analyse de la capacité

  1. Il peut y avoir plusieurs solutions en fonction de l’unité choisie pour mesurer le volume. Cependant, toutes ces solutions doivent être conciliées entre elles. Dans la présente solution, le volume sera mesuré en fonction des heures productives.


    2. Les ventes sont de 146 880 000 $, soit une moyenne de 102 000 $ par heure productive. Les coûts variables sont de 252 000 $ par jour, soit une moyenne de 42 000 $ par heure productive. La marge sur coûts variables est donc de 60 000 $ par heure productive.

    Le tableau qui suit résume le calcul des points morts pour les quatre situations demandées.

    Les ventes par heure productive restent inchangées car Capapro a dû refuser plusieurs commandes. Donc, l’augmentation des heures productives entraînera une hausse équivalente des ventes.
    Ainsi, 66 000 $ = 102 000 – ((252 000 ´ 240)/(1 440 + 240)).
     

  2. Il est impossible de les calculer parce qu’il n’y en a pas, ni dans un cas, ni dans l’autre, comme l’illustre le graphique qui suit. Ce dernier présente les droites de résultat net en fonction du volume et elles ne se croisent pas.



    3.  

  3. Construire une deuxième usine coûte toujours plus cher à l’entreprise et ne change en rien la productivité actuelle selon les données fournies. Cela permet de doubler la production et de répondre à la demande. L’augmentation du point mort, qui passe de 830 heures à 1 500 heures, s’explique par la seule augmentation des coûts fixes puisque la marge sur coûts variables est la même. Il vaudrait donc mieux ajouter un deuxième quart de travail, ce qui présente beaucoup moins de risques.
Par ailleurs, le projet de réingénierie permet d’accroître la productivité d’une heure par jour sans aucun coût additionnel pour l’entreprise. On parvient à ce résultat en transformant des heures improductives en heures productives, donc en utilisant le même personnel. Nous recommandons fortement ce projet. Ce projet combiné à l’ajout d’un deuxième quart de travail apparaît le plus intéressant pour l’entreprise qui augmenterait son nombre d’heures productives par an de 1 920, soit 1 440 heures pour un quart additionnel, plus 2 fois 240 heures pour l’augmentation d’une heure productive par quart de travail.

Exercice 7.8 Projet d’investissement et structure des coûts

1. Le tableau qui suit présente la marge sur coûts variables par unité ainsi que les coûts fixes.

Le tableau suivant présente les résultats d’une analyse CVB.

De plus, le seuil d’indifférence entre le projet et le statu quo se calcule ainsi :
23,00 $ ´ x - 16 862 750 $ = 33,80 $ ´ x - 18 230 000 $,
x = (18 230 000 $ – 16 862 750 $)/(33,80 $ - 23,00 $)
x = 126 597 unités.
 

2. Il devrait installer immédiatement l’équipement de pointe, car il ressort que l’emploi de cet équipement est nettement moins risqué en raison de l’augmentation moins élevée que prévu des frais fixes totaux. En effet, la diminution des frais généraux liés aux stocks compense en bonne partie l’augmentation des frais généraux de fabrication liés aux machines et autres frais fixes. De plus, la marge sur coûts variables augmente de façon intéressante et on quadruple la capacité de l’usine.

Exercice 7.9 Projet d’investissement et structure des coûts

1. Le tableau qui suit présente le calcul du point mort du projet.


 
  Le seuil d’indifférence entre le projet et la situation actuelle lorsqu’on considère la main-d’œuvre directe comme un coût variable est de 81 060 963 $.
0,537872007 ´ x - 34 768 000 $ = 0,746357071 ´ x - 51 668 000 $,
x = (51 668 000 $ – 34 768 000 $)/(0,746357071 – 0,537872007)
x = 81 060 963 $.

2. L’entreprise a une occasion en or de financer de nouvelles immobilisations, mais son point mort deviendra plus élevé. Elle accroîtra son risque sans améliorer sa productivité. Il faudrait qu’elle puisse profiter de l’occasion pour acquérir de l’équipement plus performant, mais elle n’est pas en mesure de le faire.

Exercice 7.10 Sous-traitance et effet sur la structure des coûts

1. Le tableau qui suit présente le calcul de la marge sur coûts variables ainsi que le montant des coûts fixes.
Le taux de 20 $ par heure pour les frais de déplacement et de représentation s’obtient en divisant e montant total de ces frais par le nombre d’heures de contrats que l’on peut retrouver en divisant le montant total des honoraires par le tarif horaire de 150 $.

Le tableau qui suit présente différents résultats de l’analyse CVB.

2. Pour réduire encore plus la vulnérabilité de l’entreprise face à des variations du nombre d’heures de contrats, on a la possibilité de réduire les frais fixes. Voici des suggestions visant cet objectif :

i) Proposer aux administrateurs une rémunération comportant une partie fixe et une autre qui serait fonction du rendement de l’entreprise. On pourrait ainsi réduire de façon importante les salaires des administrateurs.   ii) Offrir à un plus grand nombre d’ingénieurs de travailler comme pigistes. Cependant, le taux offert aux 120 des 300 ingénieurs, bien qu’il ne soit pas élevé en soi pour ce genre de travail, est trop élevé par rapport au taux de revient effectif de 65,10 $ des ingénieurs engagés par contrat annuel. L’entreprise devrait envisager une formule intermédiaire où elle offrirait 80 $ l’heure et la garantie d’un nombre minimal d’heures de contrats (1 000 heures, par exemple). Une telle proposition, tout en réduisant les frais fixes, ne perturberait pas trop la marge sur coûts variables.   iii) Quant aux frais généraux d’administration, il nous faudrait plus d’informations sur les activités qu’ils englobent pour apporter des suggestions concrètes.   Exercice 7.11 Points morts d’activités

Le tableau qui suit permet de répondre aux deux premières questions :

La réponse à la première question est de 1 227 unités par commande et la réponse à la deuxième question est de 7 421 unités par lot.

Ces deux réponses soutiennent que le coût des activités ne varie pas selon le nombre d’unités produites (ce qui est posé explicitement dans la question) mais selon le nombre d’unités de l’inducteur considéré. Par exemple, le coût de l’activité Achat et réception varie selon le nombre de commandes.

3. Il est recommander d’augmenter le nombre d’unités par commande, par lot, par nouveau produit, par heure-machine et le nombre d’unités supervisées par employé.

Exercice 7.12 Analyse CVB à deux dimensions

1. Le coût fixe des immobilisations de 4 800 000 $ correspond à une moyenne de 120 000 $ par salle, étant donné que les 40 salles seront utilisées; à 4 000 $ par salle par semaine, compte tenu de 30 semaines; à 800 $ par salle par semaine par jour, compte tenu de 5 jours par semaine et finalement à 80 $ de l’heure, compte tenu de 10 heures par jour. Le coût de 72 000 $ pour le professeur correspond à un coût de 400 $ par heure passée en classe, compte tenu de 180 heures de classe par année. 

Comme un étudiant rapporte 40 $ l’heure, nous avons besoin de 12 étudiants pour équilibrer le budget selon ces données, soit 400 $ pour couvrir le salaire du professeur et 80 $ pour couvrir les frais fixes des immobilisations.

2. a) Sachant qu’un étudiant rapporte 40 $ l’heure, 20 étudiants rapportent 800 $ l’heure, ce qui fait une marge sur coûts variables de 400 $, déduction faite du coût horaire du professeur. Compte tenu des coûts fixes de 800 $ par jour, il faudrait utiliser les salles 2 heures par jour, soit 800 $/400 $.

b) Sachant qu’un étudiant rapporte 40 $ l’heure, 15 étudiants rapportent 600 $ l’heure, ce qui fait une marge sur coûts variables de 200 $, déduction faite du coût horaire du professeur. Compte tenu des coûts fixes par jour de 800 $, nous en déduisons 4 heures, soit 800 $/200 $.

3. Dans le tableau qui suit, on calcule le coût fixe par heure en faisant varier le nombre moyen d’heures d’utilisation d’une salle de cours, le point mort en l’exprimant en nombre d’étudiants par classe, et l’excédent ou le déficit moyen par heure en faisant varier le nombre d’étudiants par classe :

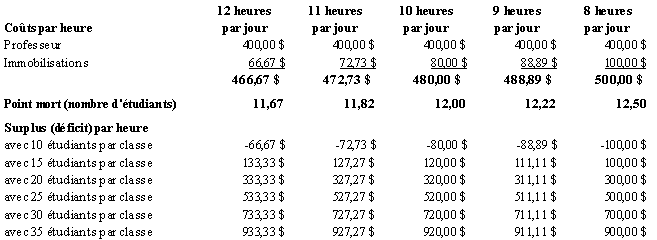
Pour équilibrer le budget, on peut augmenter le nombre d’étudiants par classe ou encore augmenter le nombre d’heures d’utilisation des salles de cours.

Exercice 7.13 Prix de vente et point mort

Le tableau qui suit permet de répondre aux deux questions.

La réponse à la question 1 est de 81 190 repas, et la réponse à la question 2 est de 63 985 repas. Toutefois, si on utilisait les valeurs arrondies de 2,68 $ et 3,40 $, on obtiendrait 81 260 repas comme réponse à la question 1 et 64 052 repas comme réponse à la question 2.

Exercice 7.14 Analyse des activités et projet d’investissement

1. L’analyse CVB commence par le calcul de la marge sur coûts variables par unité, puis par le calcul du point mort, le bénéfice à différents niveaux d’activité et, s’il y a lieu, le seuil d’indifférence et le bénéfice potentiel. Le tableau qui suit résume les principaux résultats.

2. Le tableau qui suit répond à la deuxième question.

3. Nous recommandons la mise en marche du projet de remplacement des machines, car il permet :

Nous recommandons une révision des prix de vente des produits avec prise en compte des éléments suivants : Nous recommandons également d’analyser comment l’on pourrait réduire le coût des deux processus Conception et design des versions de produits et Prise de commandes.

Exercice 7.15 Analyse des activités et projet d’investissement

1. Le tableau qui suit répond aux deux premières questions.

3. L’entreprise devrait aller de l’avant avec le projet car, bien que le volume d’activité au point mort soit plus élevé, le bénéfice espéré avec le projet est toujours plus élevé si on considère les volumes d’activité. Le seuil d’indifférence se situe à 64 000 unités, volume nettement inférieur aux volumes actuels. Le tableau qui suit appuie notre recommandation.


 

Exercice 7.16 Choix de projets d’investissement

Le premier tableau qui suit présente le calcul de la marge sur coûts variables ainsi que celui des débours fixes. Le deuxième tableau résume les résultats de l’analyse CVB. 

Compte tenu de l’évolution de la demande, résumée dans le tableau suivant : 

Nous recommandons le projet A, si la direction de l’entreprise croit pouvoir générer à moyen terme une augmentation de la demande permettant d’utiliser 70 000 heures-machines (ce qui équivaut présentement à 140 000 unités). Sinon, avec 87 500 unités, le projet B semble préférable parce qu’il pourrait suffire pour les deux prochaines années.

Exercice 7.17 Édition et point mort

1. Le tableau qui suit présente le calcul du point mort pour une première impression. Pour y arriver, on établira d’abord le montant des commissions ainsi que les droits d’auteur et enfin les coûts fixes.


 

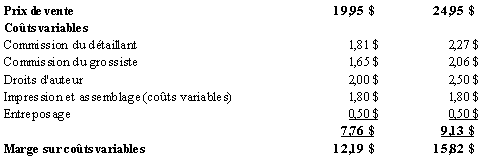
Nous avons traité le coût d’entreposage comme étant variable de 0,50 $ par unité vendue, ce qui représente une moyenne de 0,50 $ si les ventes sont distribuées uniformément et que les 1 000 unités sont vendues au cours de l’année. Si elle vendait tous les exemplaires au cours des 6 premiers mois, il faudrait utiliser 0,25 $ par unité.
 

2. Le tableau qui suit présente le calcul du point mort pour une réimpression.

Exercice 7.18 Analyse de la capacité

1. Le point mort et la marge de sécurité de l’usine 1 sont calculés ainsi :
Marge sur coûts variables en pourcentage des ventes =
(100 000 000 $ - 20 000 000 $)/100 000 000 $ = 0,8
Donc, 0,8 ´ Ventes au point mort = 60 000 000 $
Ventes au point mort = 60 000 000 $/0,8
Ventes au point mort = 75 000 000 $
Marge de sécurité = 25 000 000 $, soit 100 000 000 $ - 75 000 000 $
Le point mort et la marge de sécurité de l’usine 2 sont calculés ainsi :
Marge sur coûts variables en pourcentage des ventes =
(90 000 000 $ - 18 000 000 $)/90 000 000 $ = 0,8
Donc, 0,8 ´ Ventes au point mort = 55 000 000 $
Ventes au point mort = 55 000 000 $/0,8
Ventes au point mort = 68 750 000 $
Marge de sécurité = 21 250 000 $, soit 90 000 000 $ - 68 750 000 $
Le point mort et la marge de sécurité de l’usine 3 sont calculés ainsi :
Marge sur coûts variables en pourcentage des ventes =
(60 000 000 $ - 12 000 000 $)/60 000 000 $ = 0,8
Donc, 0,8 ´ Ventes au point mort = 40 000 000 $
Ventes au point mort = 40 000 000 $/0,8
Ventes au point mort = 50 000 000 $
Marge de sécurité = 10 000 000 $, soit 60 000 000 $ - 50 000 000 $
Le point mort et la marge de sécurité de l’ensemble du groupe sont calculés ainsi :
Marge sur coûts variables en pourcentage des ventes =
(250 000 000 $ - 50 000 000 $)/250 000 000 $ = 0,8
Donc, 0,8 ´ Ventes au point mort = 195 000 000 $, soit 155 000 000 $ + 40 000 000 $
Ventes au point mort = (155 000 000 $ + 40 000 000 $)/0,8
Ventes au point mort = 243 750 000 $
Marge de sécurité = 6 250 000 $, soit 250 000 000 $ - 243 750 000 $

2. Le point mort de l’usine 1 est calculé ainsi :
Marge sur coûts variables en pourcentage des ventes =
(100 000 000 $ - 20 000 000 $)/100 000 000 $ = 0,8
Donc, 0,8 ´ Ventes au point mort = 60 000 000 $
Ventes au point mort = 60 000 000 $/0,8
Ventes au point mort = 75 000 000 $

La fermeture de l’usine no 3 ainsi que le réaménagement du processus de production ne modifient aucunement le point mort de l’usine 1. En effet, la marge sur coûts variables en pourcentage des ventes ne change pas car elle est la même pour les trois usines, soit 0,8.

Le point mort de l’usine 2 est calculé ainsi :
Marge sur coûts variables en pourcentage des ventes =
(90 000 000 $ - 18 000 000 $)/90 000 000 $ = 0,8
Donc, 0,8 ´ Ventes au point mort = 55 000 000 $
Ventes au point mort = 55 000 000 $/0,8
Ventes au point mort = 68 750 000 $

La fermeture de l’usine 3 ainsi que le réaménagement du processus de production ne modifient aucunement le point mort de l’usine 2. En effet, la marge sur coûts variables en pourcentage des ventes ne change pas car elle est la même pour les trois usines, soit 0,8.

Le point mort de l’ensemble du groupe est calculé ainsi :
Marge sur coûts variables en pourcentage des ventes =
(250 000 000 $ - 50 000 000 $)/250 000 000 $ = 0,8
Donc, 0,8 ´ Ventes au point mort = 155 000 000 $, soit 115 000 000 $ + 40 000 000 $ puisque les coûts de transformation sont réduits de 40 000 000 $ à la suite de la fermeture de l’usine 3.
Ventes au point mort = 155 000 000 $/0,8
Ventes au point mort = 193 750 000 $

3. Le point mort de l’ensemble du groupe est calculé ainsi :
Marge sur coûts variables en pourcentage des ventes =
(250 000 000 $ - 50 000 000 $)/250 000 000 $ = 0,8
Donc, 0,8 ´ Ventes au point mort = 120 000 000 $, soit 80 000 000 $ + 40 000 000 $ puisque les coûts de transformation sont réduits de 40 000 000 $ à la suite de la fermeture de l’usine 3, de 55 000 000 $ à la suite de la fermeture de l’usine 2 et accrus de 20 000 000 $ à la suite de l’ajout d’un quart de travail à l’usine 1.

Ventes au point mort = 120 000 000 $/0,8
Ventes au point mort = 150 000 000 $

4. Le rapport au président.

Monsieur le président,

Il existe deux moyens d’améliorer le rendement financier de l’entreprise :

Ces deux stratégies peuvent être implantées par étapes.

La réingénierie du processus de production permettra d’améliorer la productivité des usines sans toutefois se traduire par un effet sur les résultats financiers actuels à cause de la méthode utilisée pour calculer ces résultats. Cependant, ce projet libérera de la capacité aux usines 1 et 2, ce qui permettra d’y récupérer la production de l’usine 3, puis de la fermer.

La fermeture de l’usine 3 permettra d’économiser 40 millions de coûts de transformation liés à son fonctionnement. La fermeture subséquente de l’usine 2 permettra d’économiser 55 millions additionnels liés à son fonctionnement; par ailleurs, ce projet engendra 20 millions de coûts additionnels à l’usine 1 relatifs à l’ajout d’un quart de travail.