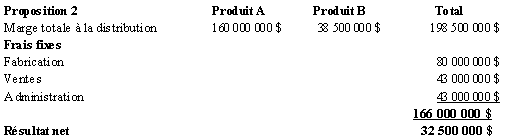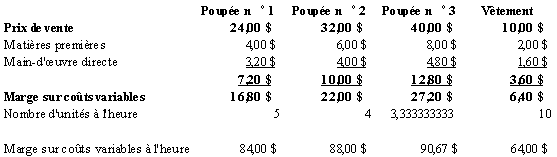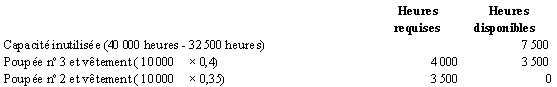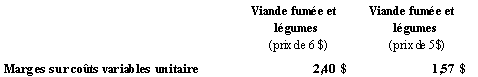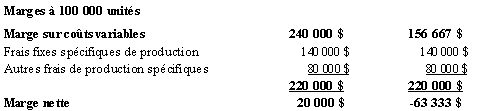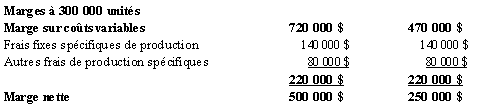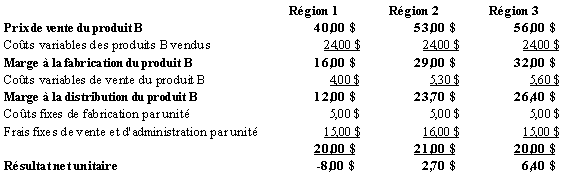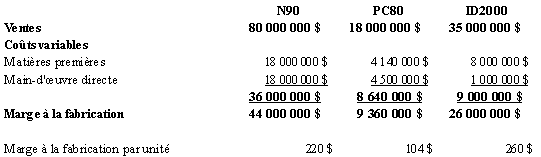Après avoir étudié ce chapitre, vous serez capable :

• de définir différentes marges;
• d’analyser les marges dans un contexte de prise de décision;
• d’appliquer la méthode des coûts variables;
• d’appliquer la méthode des coûts spécifiques;
• d’analyser certaines décisions influant sur les marges;
• d’établir une classification des décisions liées à la gestion.

Les marges sont au cœur des décisions. Comprendre les différentes marges et savoir les calculer, c’est saisir en bonne partie les conséquences financières de plusieurs décisions. Nous consacrons la première partie de ce chapitre à étudier ces notions et à les illustrer à l’aide d’exemples choisis pour leur valeur pédagogique.

Analyser les marges dans un contexte de prise de décision

Au-delà de la définition des marges, leur utilisation dans un contexte décisionnel constitue l’objectif de la première partie de cet ouvrage.

Appliquer la méthode des coûts variables

La méthode des coûts variables est centrée sur la détermination de la marge sur coûts variables. Cette méthode utilisée depuis fort longtemps pour la détermination des différentes marges témoigne de l’importance accordée à cette information. Nous la décrivons à l’aide d’exemples et nous en présentons les effets, notamment sur l’évaluation des stocks.

Appliquer la méthode des coûts spécifiques

La méthode des coûts spécifiques vise à déterminer la marge nette. Cette méthode nous donne également la comptabilité par centres de responsabilité. Nous la décrivons à l’aide d’exemples et de mises en situation illustrant des décisions typiques de gestion.

Analyser certaines décisions influant sur les marges

Le choix entre deux ou plusieurs propositions découle de tout un ensemble de décisions de gestion que nous abordons à l’aide de l’information comptable, notamment les différentes marges vues en début de chapitre. C’est une première occasion d’apprécier l’utilité de la comptabilité dans la prise de décisions de gestion.

Établir une classification des décisions liées à la gestion

Il est utile de cerner le paysage complet des décisions de gestion avant d’aborder l’analyse de décisions particulières. Notre objectif est aussi de présenter une alternative à la classification traditionnelle des décisions à court terme et des décisions à long terme.

Questions de révision

1. La marge d’un objet représente la différence entre le revenu tiré d’un objet et le coût de cet objet.

 
2. La marge à la fabrication représente le revenu variable moins les coûts variables de fabrication.

 
3. La marge à la distribution représente la marge à la fabrication moins les coûts variables de distribution.

 
4. La marge sur coûts variables représente le revenu variable moins tous les coûts variables alors que la contribution marginale représente le revenu de la dernière unité vendue moins le coût variable de cette unité.

 
5. Parce que la marge sur coûts variables est proportionnelle au volume alors que les coûts fixes ne bougent pas, et parce que tout ce qui est variable peut être influencé et que tout ce qui est fixe ne peut l’être.

 
6. La marge par unité d’un facteur de production correspond à la marge sur coûts variables exprimée en fonction d’un facteur de production.

 
7. La marge par unité d’un facteur de production est significative pour la décision lorsque le facteur de production utilisé présente une contrainte. Par exemple, la marge par heure de travail dans un atelier est significative pour la décision lorsque cet atelier fonctionne à pleine capacité.

 
8. La méthode des coûts variables consiste essentiellement à réorganiser des informations qui sont fournies aux tiers par la méthode des coûts complets; elle fournit l’information sur les différentes marges sur coûts variables, notamment la marge à la fabrication et la marge à la distribution.

 
9. La méthode des coûts variables a l’avantage de donner un aperçu de l’effet de la variation du volume sur le bénéfice.

 
10. Elle doit tenir compte de ses coûts fixes dans l’évaluation de la rentabilité des produits et des services.

 
11. La méthode des coûts variables évalue les stocks au coût variable de fabrication. De ce fait, il n’est plus possible de reporter par le biais des stocks une portion des coûts fixes de fabrication à l’exercice suivant.

 
12. La marge nette d’un produit est égale aux revenus engendrés par ce produit moins l’ensemble des coûts qui lui sont propres, ce qu’on peut exprimer de la façon suivante : Marge nette = Marge sur coûts variables spécifiques - Coûts fixes spécifiques

 
13. La méthode des coûts spécifiques cerne les coûts spécifiques à un objet de coût désigné et calcule la marge nette par rapport à cet objet de coût.

 
14. La comptabilité par centres de responsabilité consiste à rattacher à des unités administratives les coûts et les revenus qui leur sont propres.

 
15. Parce que, d’une part, dans un contexte de mondialisation des marchés, de compétitivité accrue des entreprises, d’évolution technologique de plus en plus rapide et de cycle de vie des produits et de l’équipement de plus en plus court, le qualificatif "à long terme" n’est plus guère approprié; d’autre part, parmi les décisions traditionnellement dites à court terme, plusieurs ont été automatisées et celles qui ne l’ont pas été engendrent bien souvent des conséquences à long terme.

 
16. Nous proposons la classification suivante : les décisions d’évaluation de propositions; les décisions liées au volume d’activité; les décisions requérant un financement.

 
17. L’analyse différentielle, en faisant ressortir chacun des éléments de revenus et de coûts touchés par une décision, par rapport à une situation particulière, permet de déterminer beaucoup plus rapidement l’impact d’une variation du volume d’activité sur les résultats que l’analyse globale, qui dégage les revenus totaux et les coûts totaux découlant de chacune des propositions.

 
18. Parce qu’il n’y a presque plus d’éléments de coût strictement variables et que la majorité des coûts sont fixes à court terme.

 
19. Le piège des charges fixes est de considérer le coût unitaire comme un coût variable, ce qu’il n’est pas à cause de la portion des coûts fixes répartis qui est conditionnelle à un niveau d’activité donné, soit le niveau ayant servi à calculer le coût unitaire.

 
20. Parce que les résultats quantitatifs sont toujours soumis à des hypothèses de comportement des personnes. Ces résultats ne seront intéressants et s’avéreront utiles que si l’analyste a su poser les bonnes hypothèses, notamment en ce qui concerne l’analyse stratégique.

Exercice 6.1 Marge sur coûts variables

1. Le tableau qui suit résume le calcul de la marge sur coûts variables des deux produits.


 
 

2. La marge sur coûts variables de P2 augmente de 50 $ par unité puisque le coût de la main-d’œuvre directe est réduit des deux tiers. Comme elle fabrique et vend 40 000 unités de P2, l’entreprise économisera 2 000 000 $, ce qui fait plus que compenser l’augmentation des frais fixes de fabrication de 1 000 000 $.

 
3. Si on ramène les prix de P1 et de P2 aux prix moyens du marché, les marges sur coûts variables de P1 et de P2 diminueront respectivement de 30 $ par unité. Comme elle fabrique et vend 30 000 unités de P1, l’entreprise subira une diminution de revenus provenant de P1 de 900 000 $ et, comme elle fabrique et vend 40 000 unités de P2, l’entreprise subira une diminution de revenus provenant de P2 de 1 200 000 $, ce qui fait une diminution totale de 2 100 000 $ alors que ses coûts diminueront de 2 000 000 $. Donc, strictement sur le plan économique, la proposition de la directrice du marketing n’est pas avantageuse. Par ailleurs, la perte relative à ce projet n’est pas énorme, soit 100 000 $; et si le projet permet à l’entreprise de garder ses parts de marché, voire de les augmenter, il faut probablement aller de l’avant. On ne peut conclure avant d’avoir analysé l’effet de ce projet sur les parts de marchés.

 

Nous avons préparé deux budgets pour conseiller cette jeune comptable :

Si l’on considère strictement les 3 000 heures des contrats qu’elle détient, il est préférable d’embaucher un analyste à l’année et un autre à l’heure. Cependant, cette situation pourrait changer rapidement si elle décrochait d’autres contrats.

Il est préférable de raisonner à partir de la marge sur coûts variables unitaires et des coûts fixes. La marge sur coûts variables unitaires est de 150 $ l’heure pour un analyste embauché à l’année et de 100 $ l’heure pour un analyste embauché à l’heure.

Exercice 6.3 Modification d’activités et analyse différentielle

Le tableau qui suit résume l’effet du projet étudié sur les coûts.

En plus de diminuer ses coûts de 1 858 600 $, l’entreprise sera en mesure de réduire son fonds de roulement d’un montant équivalent à 60% du stock de produits finis.

Exercice 6.4 Marge sur coûts variables

La marge sur coûts variables actuelle est de 6,60 $ pour un contenant de 40 L, soit 15,60 $ de revenu moins 9,00 $ de coûts variables. Le revenu de 15,60 $ se calcule ainsi,

15,60 $ = (40 ´ 0,75 ´ 0,50 $) + (40 ´ 0,15 ´ 0,10 $).

Comme l’entreprise paierait 4 $ de plus par contenant de 40 L, la marge sur coûts variables serait de 2,60 $ le contenant de 40 L. Comme la marge est toujours positive, on peut affirmer que sur le plan strictement économique, l’offre faite à Pétrogas est intéressante.

L’entreprise fonctionne actuellement à 80% de sa capacité. Elle traite un volume de 80 000 contenants, qui correspond à 3 200 000 L. Accepter l’offre de 800 000 L lui permettrait de fonctionner à 100% de sa capacité. Toutefois, il ne faudrait pas que ses autres fournisseurs de qui elle s’approvisionne en ne payant que 8 $/40 L apprennent que Pétrogas paie 12 $/40 L, sinon elle risque de les indisposer et de voir son coût d’approvisionnement augmenter substantiellement.

Exercice 6.5 Choix de la marge sur coûts variables

Le tableau qui suit présente les différentes marges sur coûts variables. Ces données nous permettront d’évaluer les deux propositions.

1. La première proposition est intéressante car elle augmente le résultat net de l’entreprise de 20 500 000 $, ce qui le porte à 54 000 000 $ comme le démontre le tableau suivant.



La marge à la distribution du produit A se calcule ainsi :
136 000 000 $ = 4 000 000 unités ´ 34 $/unité où 34 $ = 70 $ - 36 $.

La marge à la distribution du produit B se calcule ainsi :
29 000 000 $ = 500 000 unités ´ 58 $/unité où 58 $ = 110 $ - 52 $.

Par ailleurs, l’entreprise perd le contrôle de l’activité de distribution et devra dorénavant compter sur un distributeur. L’augmentation estimée du bénéfice devra compenser la perte de contrôle.
 

2. La deuxième proposition n’est pas intéressante, car elle réduit le résultat net de l’entreprise de 1 000 000 $, ce qui le fait tomber à 32 500 000 $ comme le démontre le tableau suivant.

 

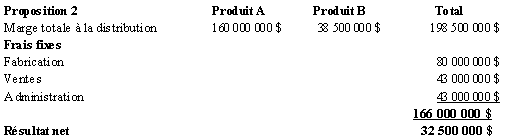
La marge à la distribution du produit A se calcule ainsi :
160 000 000 $ = 4 000 000 unités ´ 40 $/unité.

La marge à la distribution du produit B se calcule ainsi :
38 500 000 $ = 500 000 unités ´ 77 $/unité où 77 $ = 140 $ - 44 $ - 19 $.

Exercice 6.6 Méthode du coût complet et méthode des coûts variables

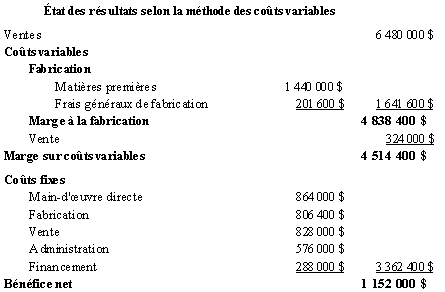
2. Le tableau qui suit présente le calcul du bénéfice net estimé si l’entreprise ne fabrique que 132 000 unités l’an prochain.


 

3. Le tableau qui suit présente le calcul du bénéfice net estimé si l’entreprise ne fabrique que 132 000 unités l’an prochain et si elle opte pour la rémunération au taux de 20 $ l’heure.


 

4. Le contrat annuel permet généralement d’obtenir un coût moyen à l’heure moins élevé tout en s’assurant la fidélité du personnel.

Exercice 6.7 Effet d’un accroissement de stock sur le résultat net

1. Le tableau qui suit présente les résultats selon la méthode des coûts variables.

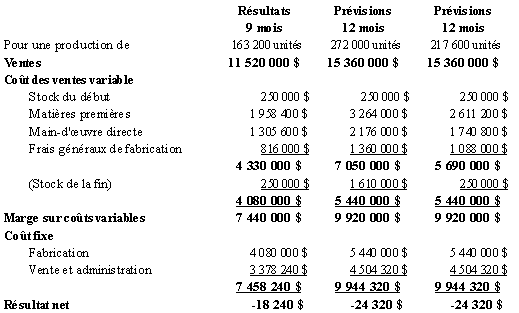
Le résultat net est le même, que l’entreprise produise 272 000 unités ou 217 600 unités dans l’année. Cela s’explique par le fait que les stocks sont calculés à leurs coûts variables et que tous les coûts engagés dans l’année sont considérés comme des charges de l’exercice.

Exercice 6.8 Effet d’une diminution de stock sur le résultat net

1. Le tableau qui suit présente le résultat net prévu, si le directeur général décide de maintenir le stock de clôture à 96 600 unités.

 
2. Le tableau suivant présente le résultat net de l’exercice en cours ainsi que le résultat net prévu. On suppose que le stock est ramené à 15 000 unités à la fin du prochain exercice.

 


 

3. Au volume d’activité qui permettrait de ramener le stock à 15 000 unités, la marge sur coûts variables ne couvre même pas les coûts fixes engagés. Le résultat net serait pire si on calculait ce résultat avec la méthode du coût complet, car l’entreprise supporterait, en plus des coûts fixes de fabrication de l’exercice en cours, une portion des coûts fixes de fabrication de l’exercice précédent, coûts qui sont de 6 528 000 $.

Exercice 6.9 Marge par unité d’un facteur de production

1. Le tableau qui suit illustre le calcul de la marge sur coûts variables ainsi que la marge sur coûts variables à l’heure.

Le tableau qui suit permet de répondre aux deux premières questions, car il présente la marge sur coûts variables par unité produite et la marge sur coûts variables par heure de main-d’œuvre directe.

 
Exercice 6.11 Marge par unité d’un facteur de production

 
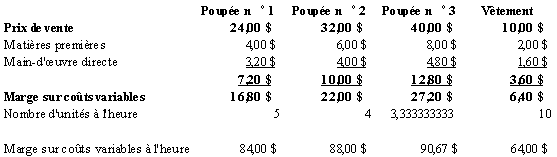
On doit fabriquer en priorité les produits dont la marge sur coûts variables à l’heure est la plus élevée tout en respectant les trois contraintes. Le tableau qui suit présente ces calculs.
 

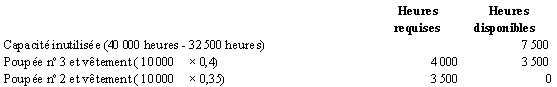
Il faut donc accepter les commandes additionnelles de 10 000 poupées n^o 2, de 10 000 poupées n^o 3 et de 20 000 vêtements.

2. Le bénéfice qui découlerait de l’acceptation de ces commandes additionnelles correspond à l’augmentation de la marge sur coûts variables, soit 620 000 $. Ce montant se calcule ainsi :

620 000 $ = 10 000 ´ (27,20 $ + 6,40 $) + 10 000 ´ (22,00 $ + 6,40).
 
3. L’annulation de la confection de 20 000 vêtements libérera 2 000 heures de production. La capacité ainsi libérée permettra de fabriquer des poupées n^o 1, les seules dont la demande n’est pas totalement satisfaite. Or, avec 2 000 heures, on peut fabriquer 6 666 poupées n^o 1 et vêtements, car il ne faut pas oublier de les vêtir. Le calcul est le suivant :

6 666 = 2 000 heures/ (0,25 + 0,1).
 
4. L’annulation de 20 000 vêtements n’aura-t-il pas un effet négatif sur la vente des poupées? Il y a actuellement au moins 20 000 clients sur les 90 000 acheteurs de poupées, soit plus de 20 % qui achètent plus d’un vêtement.

1. Le tableau qui suit présente la marge nette aux prix demandés de 6 $ et de 5 $ ainsi qu’au trois volumes d’activité de 100 000, 200 000 et de 300 000 unités.








 

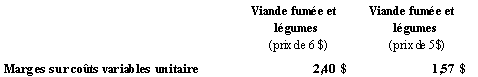
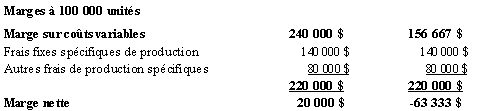
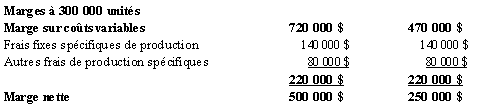
2. À l’exception des coûts fixes spécifiques, les coûts fixes communs demeurent, que le produit soit ou non lancé. Les coûts communs à l’ensemble des produits de l’entreprise sont répartis entre l’ensemble des produits selon une base proportionnelle au volume.

Exercice 6.13 Coûts spécifiques et marges nettes

1. Le tableau qui suit présente le calcul de la marge nette unitaire pour chacune des familles de produits et pour chacun des volumes d’activité.

1. Le tableau qui suit présente le calcul de la marge nette pour chacun des produits dans chacune des régions.





 

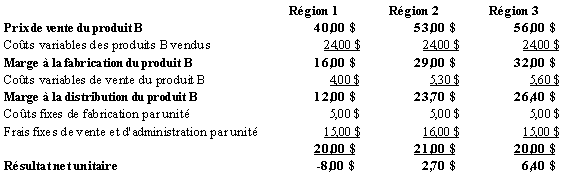
2. Les tableaux qui suivent présentent les diverses simulations du contrôleur.

La perte de 16 000 $ s’explique par le calcul suivant :
- 16 000 $ = (30 000 ´ -27,14 $) + (30 000 ´ 9,06 $) + (20 000 ´ 17,26 $) + (20 000 ´ 0,56 $) + (40 000 ´ 4,26 $).

La diminution du résultat net, qui est maintenant de 584 000 $, s’explique par le calcul suivant :
584 000 $ = (30 000 ´ 7,11 $) + (20 000 ´ 15,31 $) + (20 000 ´ -1,39 $) + (40 000 ´ 2,31 $).

La diminution du résultat net, qui est maintenant de 110 000 $, s’explique par le calcul suivant :
110 000 $ = (30 000 ´ -5,58 $) + (20 000 ´ 13,29 $) + (40 000 ´ 0,29 $).

Le résultat net de – 56 000 $ s’explique par le calcul suivant :
-56 000 $ = (20 000 ´ 7,73 $) + (40 000 ´ -5,27 $).

 
Exercice 6.15 Marges et commandes spéciales

1. Le tableau qui suit présente les différentes marges.


 

Le tableau qui suit présente le calcul du prix de la commande spéciale.



L’effet sur le bénéfice aurait été une diminution de 610 000 $ si l’entreprise avait obtenu la commande au prix habituel de la soumission. Par contre, elle ne réalise qu’un bénéfice de 30 000 $ sur cette commande, soit le montant de la marge à la distribution, laquelle se calcule ainsi : 30 000 $ = 1 830 000 $ - 1 800 000 $.
 

2. Les règles ne se justifient que par les moyennes et le montant suffisamment élevé des commandes. Lorsque le montant des commandes varie, les grosses commandes sont désavantagées par cette règle, car elles assument un plus grand poids des coûts indirects alors que les petites commandes n’en assument presque pas.

Le tableau qui suit présente les marges sur coûts variables des produits actuels et futurs de l’entreprise NPI ltée.

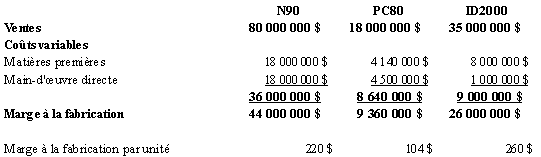
Si le produit ID2000 est lancé en remplacement du produit PC80, le bénéfice de l’entreprise pourrait augmenter de 4 460 000 $, comme le démontre le tableau suivant :

Les frais de 6 millions de dollars liés à la recherche et au développement n’ont pas été pris en compte dans ce calcul parce qu’ils ne sont pas liés à cette décision. En effet, ils ont déjà été engagés.

De plus, dans ce domaine, l’innovation est un facteur de succès reconnu. Rien ne garantit que les ventes de PC80 vont se maintenir au volume actuel.

Exercice 6.17 Marges et commande spéciale

Monsieur le président,

Strictement sur le plan économique, vous devriez accepter cette commande spéciale, car votre entreprise en tirera un bénéfice additionnel de 280 000 $. Ce résultat représente un rendement de plus de 23 % par rapport au montant de la commande, ce qui est excellent si on le compare au rendement de l’entreprise qui est de 11 %.

Le tableau qui suit résume nos calculs :

Par ailleurs, cette commande ne doit en aucune façon modifier les ventes courantes. Il ne faut pas que les clients habituels s’interrogent sur le prix de 60 $ consenti à ce client très spécial. De plus, il ne faut pas que ce dernier viennent offrir les tables sur le même marché que vos clients habituels.

Exercice 6.18 Marges et ventes interdivisionnaires