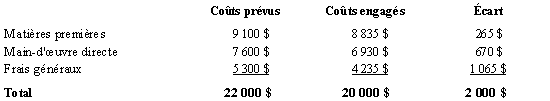Chapitre 3
Le coût de revient
Objectifs

    Après avoir étudié ce chapitre, vous serez capable :

Expliquer ce qu’est le coût de revient

Il existe plusieurs types de coûts de revient; il est donc utile de les expliquer à l’aide d’exemples ainsi que de commenter l’interprétation à donner à la définition proposée.

Calculer des coûts de revient simples

La véritable connaissance des coûts implique la maîtrise de calculs simples. C’est par le biais des 15 exemples et des 27 exercices que les étudiants atteindront cet objectif.

Choisir une méthode de calcul appropriée au contexte

Il existe plusieurs méthodes de calcul de coûts de revient. Ces méthodes ont été mises au point pour répondre à un besoin qui n’était pas comblé, dans un contexte particulier par les méthodes existantes. En détectant ces besoins et en les associant aux méthodes de calcul des coûts, nous serons en mesure de mieux les adapter au contexte dans lequel nous nous trouverons.

Analyser des décisions influant sur les coûts

Replacer le calcul du coût de revient dans son véritable cadre, celui de la prise de décisions de gestion.

Interpréter les coûts de revient dans un cadre de prise de décision

C’est dans les exercices que l’on rencontre les subtilités, les avantages et les limites de chaque méthode de calcul.

Questions de révision

1. Le coût d’un objet est la somme de toutes les ressources consommées par cet objet.

2. Le coût de revient d’un objet est la somme de toutes les ressources consommées par cet objet. Cependant, on parle de coût de revient lorsqu’il y a eu transformation de ressources ou que le lien n’est pas direct entre les ressources utilisées pour l’obtenir et l’objet et qu’il a fallu manipuler des données.

3. a) L’assemblage d’un vélo : des pièces, du temps de main-d’œuvre, l’utilisation d’un atelier, de machines, d’outils ainsi que de fournitures.

   b) La fabrication d’un costume taillé sur mesure : du tissu, du temps de main-d’œuvre, l’utilisation d’un atelier, de machines, d’outils ainsi que de fournitures.

   c) Les services reçus au cours d’une journée à l’hôpital : du temps de main-d’œuvre, des appareils et un local.

   d) La réalisation d’un contrat de voirie pour la réfection d’un pont : des matériaux, du temps de main-d’œuvre et de l’équipement.

   e) La conception et la mise en œuvre d’un programme de prévention du crime : du temps de main-d’œuvre, du matériel de bureaux et un local.

4. On peut déterminer plusieurs coûts de revient pour un objet. Il y a le coût direct et le coût complet; il y a le coût réel et le coût prévisionnel; et, il y a le coût partiel et le coût global ainsi que le coût standard, le coût cible et le coût selon le cycle de vie du produit.

5. Les trois éléments classiques du coût de revient de fabrication sont :

a) les matières premières;
b) la main-d’œuvre directe;
c) les frais généraux de fabrication. 6. Le coût direct désigne le coût de toutes les ressources directement affectées à la production d’un bien ou d’un service; le coût indirect désigne le coût des ressources servant à la production de divers biens comme l’équipement et les immobilisations en général.

7. Le coût de transformation représente le coût de toutes les ressources ayant servi directement ou indirectement à transformer les matières premières en produits finis. Il exclut donc le coût des matières premières.

8. Dans les industries traditionnelles, le coût de transformation comprend un fort pourcentage de main-d’œuvre directe, souvent supérieur à 80 %. Par contre, la main-d’œuvre directe a presque disparu dans certaines industries de pointe, le pourcentage est souvent inférieur à 20 %.

9. Le coût complet inclut à la fois le coût des matières premières et celui de leur transformation, ce dernier comprenant une juste part des coûts indirects.

10. Le coût standard serait, selon les études des ingénieurs, le coût tel qu’il serait dans des conditions idéales, c’est-à-dire lorsque la production est efficace, efficiente et économique.

11. Comme son nom l’indique, le coût cible est un objectif, un coût qu’on cherche à atteindre pour un produit en phase de développement.

12. Le prototype ne sera mis en production que lorsqu’on aura réussi à concevoir un modèle et un procédé de fabrication correspondant aux objectifs de coûts fixés pour le produit fini.

13. Ce coût est égal à la somme de tous les coûts engendrés par un produit durant sa vie.

14. C’est important parce qu’il est possible de concevoir des produits dont le coût est peu élevé mais dont les coûts d’entretien par la suite sont relativement élevés et à l’inverse, parce qu’il est possible de concevoir des produits coûteux à l’achat mais dont les coûts d’entretien sont peu élevés.

15. La fiche de coût de revient d’un produit comprend la présentation détaillée de tous les éléments de coûts, notamment dans le cas d’un produit fabriqué :

a) la quantité et le prix des matières premières;
b) le temps et le taux de la main-d’œuvre directe;
c) la part des frais généraux attribués à ce produit, ainsi que le mode d’attribution de ces frais. 16. Les trois principaux éléments qui caractérisent les systèmes de production sont : a) le mode de fabrication;
b) le type d’organisation du travail;
c) les méthodes de déclenchement de la production. 17. Les trois principaux modes de fabrication sont : a) la fabrication sur commande;
b) la fabrication par lot;
c) la production uniforme et continue. 18. Voici quatre caractéristiques d’un produit fabriqué sur commande : a) il est fait sur mesure;
b) il est unique, conforme au devis du client;
c) il est souvent vendu au moyen d’une soumission;
d) il est parfois trop coûteux pour être stocké. 19. La construction d’un télésiège et la construction de gouttières faites sur mesure constituent deux exemples de produits faits sur mesure. Le télésiège (la longueur du câble, la force du moteur, le nombre de tours, le nombre de poulies par tour et le nombre de chaises) est fonction de la montagne (sa hauteur, son profil) où il sera installé. La gouttière est fonction de la longueur du rebord de la toiture où elle sera installée.

20. Voici quatre caractéristiques d’un produit fabriqué par lot :

a) il est constitué de plusieurs unités répondant à un devis commun;
b) il comporte des unités requérant des ressources et des procédés à peu près identiques;
c) il entraîne un démarrage de la fabrication qui nécessite la préparation de la mise en course;
d) le processus de fabrication se subdivise en plusieurs étapes. 21. L’automobile et un meuble sont généralement fabriqués par lot parce qu’ils ne sont pas personnalisés et n’ont pas besoin de l’être.

22. Voici trois caractéristiques d’un produit issu d’un processus de production uniforme et continue :

a)    l’usine fabrique des quantités ou des volumes importants d’un seul produit;
b)    le produit est souvent transformé plutôt qu’assemblé ou fabriqué;
c)    le produit est fabriqué au cours d’une opération continue.

   23. La peinture et l’essence pour les automobiles sont deux exemples de produits issus d’un processus de production uniforme. Il en est de même pour tous les produits raffinés et, la plupart du temps, de la transformation des matières premières.

24. Nous reconnaissons le type d’aménagement linéaire ou par aire de travail qui présente un flot d’opérations discontinu et le type d’aménagement cellulaire ou fonctionnel qui présente un flot d’opérations continu.

25. Le processus de fabrication juste-à-temps décrit un contexte où le délai entre le début de la production d’un article ou service donné, et son achèvement, est réduit au minimum. Lorsqu’il s’agit de produits, il n’y a pas, à toutes fins pratiques, de produits en cours.

26. Dans le cas d’un processus de production dit juste-à-temps, le délai de production de même que les stocks de produits en cours sont réduits au minimum.

27.     a) Selon l’approche de la poussée, la production est déclenchée par un ordre de travail envoyé à la première aire de travail et poussée de l’une à l’autre selon la séquence planifiée.

b) Selon l’approche de l’attraction, l’ordre de travail est envoyé à la dernière aire de travail dans la chaîne (plutôt qu’à la première), s’il s’agit d’un aménagement linéaire, ou à la fin du processus (plutôt qu’au début), s’il s’agit d’un aménagement cellulaire ou fonctionnel. La production est ainsi tirée à rebours, de la fin du processus vers le début.
  1. Voici cinq méthodes de calcul du coût de revient de fabrication :

    2.  

     
     
     
     
     

    a)    la méthode fondée sur la somme des ressources engagées dans la production;
    b) la méthode fondée sur la nomenclature de fabrication;
    c) la méthode fondée sur les centres de coûts;
    d) la méthode fondée sur une analyse d’équivalence;
    e) la méthode fondée sur une répartition par activités.

29. Voici trois caractéristiques de la méthode selon la somme des ressources engagées : a) elle est simple;
b) elle est fondée sur des données historiques;
c) elle est conçue pour un seul produit qui n’est ni décomposé en parties, ni fabriqué ou assemblé en un lieu physique unique. 30. La nomenclature d’assemblage d’un produit contient la liste de tous les composants d’un produit.         31. Voici trois caractéristiques de la méthode selon la nomenclature de fabrication :
                    a) elle requiert un devis détaillé du produit;
                    b) elle convient particulièrement à l’établissement d’un coût prévisionnel;
                    c) elle est appropriée dans le cas des produits faits sur mesure ou du mode de fabrication sur commande. 32. Voici deux exemples de centres de coûts : a) un atelier de production dans une usine ou encore l’usine en entier;
b) un service (dans un hôpital, une école, etc.) dont le directeur doit respecter un budget. 33. Voici trois caractéristiques de la méthode selon les centres de coûts : a) elle rattache les coûts à des centres, puis aux produits;
b) elle fait intervenir une répartition simple par étape;
c) elle ajoute une autre dimension à la méthode de calcul fondée sur la somme des ressources engagées dans la production. 34. On doit utiliser la méthode fondée sur une analyse d’équivalence lorsqu’on fabrique plusieurs produits différents ou lots de produits différents.

35. Voici deux caractéristiques influant sur le coût de revient :

a) des services : la grande variété de produits souvent personnalisés dont les aspects professionnels et la qualité sont liés et le coût des matières premières négligeable, mais les frais généraux élevés;
b) des projets : ils sont uniques, souvent faits pour la première fois, donc sans données historiques et peu susceptibles de se répéter, et ils sont souvent de longue durée;
c) des programmes : ils combinent à la fois les caractéristiques des services et des projets, ils nécessitent souvent un financement à caractère politique et comportent des coûts relevant de décisions politiques. 36. On doit préciser les objectifs d’information que l’on poursuit et l’utilisation que l’on souhaite faire de l’information ainsi obtenue.
  1. Voici trois catégories de décisions concernées par le coût de revient :

    2.  

     
     
     
     
     

    a) l’établissement du prix de vente;
    b) l’évaluation des stocks;
    c) l’évaluation de la rentabilité des produits et des services.

38. Dans le cas de nouveaux produits pour lesquels il n’y a aucun point de repère sur le marché, il est crucial de produire un coût de revient estimatif.

39. Oui, on peut concevoir la rentabilité moyenne à court terme, à moyen et à long terme ainsi que la rentabilité marginale d’un produit ou d’un service.

 Exercices

Exercice 3.1

Voici un tableau illustrant le calcul du coût de revient d’une vis, d’un clou, d’un boulon, puis d’une boîte de vis, d’une boîte de clous et d’une boîte de boulons :





Exercice 3.2

Le tableau suivant présente le calcul du coût de revient du projet :







La ville a respecté son budget de 125 000 $.

Exercice 3.3

Les calculs du tableau suivant permettent de répondre aux trois questions :







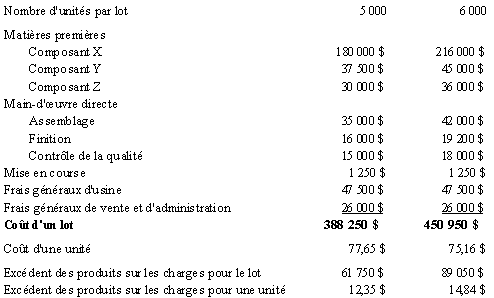
Le coût de revient unitaire prévu est de 77,65 $. Si l’entreprise décidait de fabriquer un lot de
6 000 unités, il serait de 75,16 $ par unité. Quant à l’excédent des produits sur les charges, il serait de 61 750 $ pour un lot de 5 000 unités, soit 12,35 $ par unité en moyenne, et de 89 050 $ pour un lot de 6 000 unités, soit 14,84 $ par unité en moyenne. Le coût de fabrication par unité serait de 72,45 $ pour un lot de 5 000 unités, et de 70,83 $ pour un lot de 6 000 unités.

Exercice 3.4

Voici le coût de revient global du contrat prévu initialement:

Les coûts engagés après trois semaines totalisent 77 250 $. Si on extrapole linéairement ce montant sur quatre semaines, on obtient 103 000 $:







Exercice 3.5

Le tableau suivant établit la liste des coûts relatifs à ce contrat.

Exercice 3.6
 

Selon le tableau suivant, le coût unitaire prévisionnel est de 39,88 $ et l’entreprise ne devra pas modifier son prix de vente pour obtenir une marge bénéficiaire brute de 25 %.
 
Volume prévu
50 000 
Matières premières
    Matière X
300 000 
 $
    Matière Y
240 000 
 $
    Matière Z
210 000 
 $
Main-doeuvre directe
    Atelier d'assemblage
700 000 
 $
    Atelier de finition
300 000 
 $
Frais généraux
    Dotation à l'amortissement de l'usine
33 000 
 $
    Dotation à l'amortissement des équipements
39 000 
 $
    Salaires des superviseur
123 000 
 $
    Maintenance et entretien
12 000 
 $
    Électricité
10 800 
 $
    Assurances et taxes foncières
20 500 
 $
    Fournitures d'usine
    5 500 
 $
Total
1 993 800 
 $
Coût unitaire
39,876 
 $
Prix souhaité (39,876 / 0,75)
53,17 
 $

Comme le prix souhaité est supérieur à 50 $, il est nécessaire de modifier le prix de vente pour obtenir une marge bénéficiaire de 25 %.

Exercice 3.7

Le tableau suivant présente le coût de chaque commande fabriquée durant le trimestre ainsi que le coût unitaire de chaque modèle fabriqué :

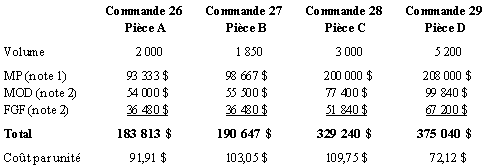
Note 1: Le coût des matières premières et de la main-d’œuvre directe a été établi à partir des quantités suivantes, c’est-à-dire au prorata des quantités utilisées.
  Note 2: Les frais généraux ont été établis en fonction des pourcentages indiqués dans la question, soit 19 %, 19 %, 27 %, et 25 %. Exercice 3.8

Voici la solution si l’on présume que la marge bénéficiaire de 20 % est calculée à partir des coûts spécifiques à un contrat, c’est-à-dire à partir de tous les coûts énumérés à l’exception des frais généraux (d’administration) de l’entreprise, communs à tous les projets.

Première partie
Le tableau suivant permet de répondre aux questions de la première partie.

Deuxième partie
Selon le tableau suivant, le bénéfice net de M. Martin avant impôt est de 403 000 $. Ce montant aurait été de 805 600 $ s’il avait soumissionné toujours en considérant une marge bénéficiaire de 20 % des charges spécifiques des contrats.
 
 

La méthode employée ici est simple. Toutefois, les frais généraux rattachables aux contrats peuvent s’avérer difficiles à estimer.

Exercice 3.9

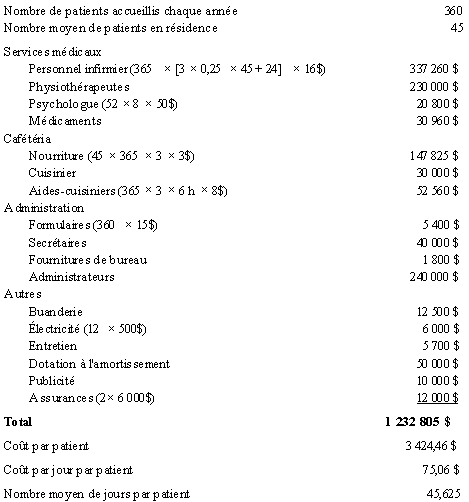
Selon le tableau suivant, le coût d’exploitation de la maison Desroches a été de 1 232 805 $ lors du dernier exercice. Le coût de revient, par jour, par patient, a été de 75,06 $, et le coût par patient accueilli a été de 3 424,46 $.







Exercice 3.10

Le tableau suivant présente la fiche du coût de revient détaillé du produit Bêta.







Exercice 3.11

Le coût de revient d’un meuble est la somme du coût de toutes les pièces du meuble ajoutée au coût d’emballage du meuble.

Exercice 3.12

Voici le tableau du coût total de toutes les pièces achetées pour 1 000 jeux de hockey. On remarque que l’entreprise achète toujours un peu plus de pièces que le nombre requis. La raison est qu’elle doit parfois remplacer certaines pièces défectueuses ou mettre de côté des pièces qui ne semblent pas répondre aux standards de qualité. Nous avons divisé le coût total des pièces par 1 000. Nous pourrions procéder différemment en calculant le coût des pièces commandées en sus du nombre exact requis et considérer ce coût au même titre que les frais généraux.

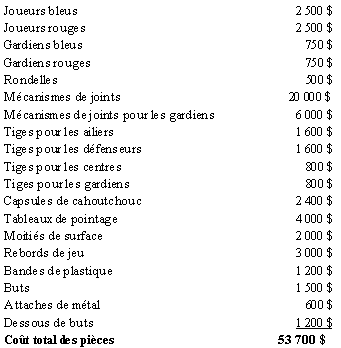
Voici le coût d’un jeu :

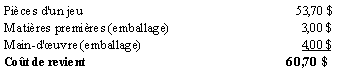
Voici le calcul du coût de revient en isolant le coût des pièces de remplacement. Le coût unitaire des pièces est alors le suivant :


 

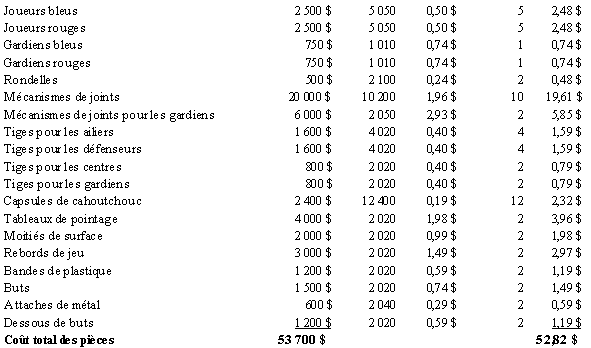
Et, le coût de revient est alors calculé ainsi :

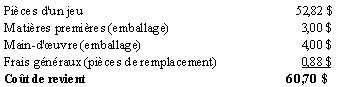
Exercice 3.13

Selon le tableau suivant, le coût de revient du lot 1 est de 130 480 $, et celui du lot 2, de
171 570 $. Le profit unitaire d’un produit du lot 1 est de 9,76 $, et celui d’un produit du lot 2, de 35,62 $.







Exercice 3.14

Le tableau suivant résume les calculs.

 

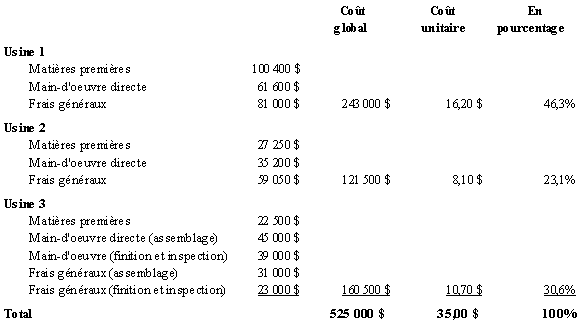
Durant le mois de septembre, le coût de revient unitaire des moteurs assemblés à l’usine 1 a été de 16.20 $. Celui des boîtiers fabriqués à l’usine 2 a été de 8,10 $. Enfin, celui des purificateurs d’air a été de 35 $, dont 10,70 $ de coûts ajoutés à l’usine 3 (ce qui représente 30,6 % du coût total).

Exercice 3.15

Comme P2 consomme trois fois plus de matières premières par unité que P1, dans chacun des trois ateliers, on peut établir l’équivalence suivante :

3 unités de P1 = 1 unité de P2
2 700 unités de P1 = 900 unités de P2
800 unités de P1 + 900 unités de P2 = 800 unités de P1 + 2 700 unités de P1
soit 3 500 unités de P1

Le tableau suivant présente le calcul du coût de revient d’une unité équivalente.

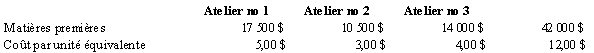
Comme 3 unités de P1 égalent 1 unité de P2, le coût par unité de P2 est respectivement de 15 $, 9 $ et 12 $ pour chacun des ateliers.
 

Exercice 3.16

Comme P2 consomme deux fois plus de temps par unité que P1 dans les ateliers nos 1 et 2, on peut établir l’équivalence suivante :

2 unités de P1 prennent le même temps que 1 unité de P2
2 unités de P1 = 1 unité de P2
1 400 unités de P1 = 700 unités de P2
500 unités de P1 + 700 unités de P2 = 500 unités de P1 + 1 400 unités de P1
soit 1 900 unités de P1

Dans l’atelier no 3, les unités de P1 et P2 sont équivalentes, on compte donc 1 200 unités, soit 500 unités de P1 + 700 unités de P2.

Le tableau suivant présente le calcul du coût de revient de la main-d’œuvre directe d’une unité équivalente.

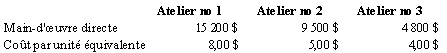
Dans les ateliers nos 1 et 2, comme 2 unités de P1 égalent 1 unité de P2, une unité de P2 coûte 16 $ et 10 $ respectivement. Le coût par unité de la main-d’œuvre de P2 dans les trois ateliers est donc de 30 $.

Le coût par unité de la main-d’œuvre de P1 dans les trois ateliers est donc de 17,00 $.

Le tableau qui suit présente une conciliation de ces réponses.

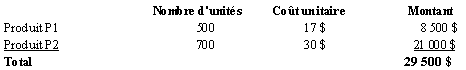
Exercice 3.17

Comme P2 consomme quatre fois plus de temps-machine par unité que P1, on peut établir l’équivalence suivante :

4 unités de P1 prennent le même temps-machine que 1 unité de P2
4 unités de P1 = 1 unité de P2
1 200 unités de P1 = 300 unités de P2
700 unités de P1 + 300 unités de P2 = 700 unités de P1 + 1 200 unités de P1
soit 1 900 unités de P1

Le tableau suivant présente le calcul du coût de revient de transformation d’une unité équivalente.

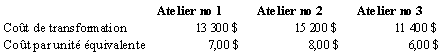
Le coût de transformation par unité de P1 dans les trois ateliers est donc de 21,00 $, et celui de P2, quatre fois plus, soit 84 $.

Le tableau qui suit présente une conciliation de ces réponses.

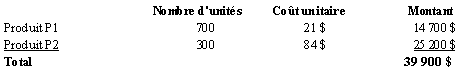
Exercice 3.18

Comme P2 nécessite deux fois plus de temps-machine par unité que P1 en ce qui a trait au coût de transformation, on peut établir l’équivalence suivante :

2 unités de P1 prennent le même temps-machine que 1 unité de P2
2 unités de P1 = 1 unité de P2
1 600 unités de P1 = 800 unités de P2
600 unités de P1 + 800 unités de P2 = 600 unités de P1 + 1 600 unités de P1
soit 2 200 unités de P1

En ce qui a trait à la consommation des matières premières, les unités sont équivalentes.

Le tableau suivant présente le calcul du coût de revient de transformation d’une unité équivalente.

Le coût de revient de P1 est donc de 19 $, soit 10 $ + 9 $, et celui de P2, de 28 $, soit 10 $ + 2 ´ 9 $.

Le tableau qui suit présente une conciliation de ces réponses.

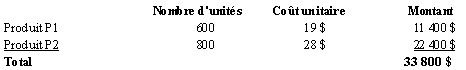
Exercice 3.19

Comme P2 coûte deux fois plus cher par unité que P1 à l’usine no 3, on peut établir l’équivalence suivante :

2 unités de P1 présente le même coût que 1 unité de P2
2 unités de P1 = 1 unité de P2
800 unités de P1 = 400 unités de P2
500 unités de P1 + 400 unités de P2 = 500 unités de P1 + 800 unités de P1
soit 1 300 unités de P1
Le tableau suivant présente le calcul du coût de revient d’une unité équivalente à l’usine no 3.

De plus, le coût de revient du produit P1 à l’usine no 1 est de 8 $, soit 4 000 $/500 unités, et celui du produit P2 à l’usine no 2, de 10 $, soit 4 000 $/400 unités.

Donc, le coût de revient du produit P1 est de 14 $, soit 8 $ + 6 $, et celui du produit P2, de 22 $, soit 10 $ + 2 ´ 6 $.

Le tableau qui suit présente une conciliation de ces réponses.

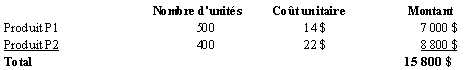
Exercice 3.20

Comme les matières premières de P1 coûtent deux fois plus cher le kilogramme que celles de P2, on peut établir l’équivalence suivante :

2 unités de P2 prennent la même quantité de matières premières que 1 unité de P1
2 unités de P2 = 1 unité de P1
4 000 unités de P2 = 2 000 unités de P1
1 500 unités de P2 + 2 000 unités de P1 = 1 500 unités de P2 + 4 000 unités de P2
soit 5 500 unités de P2
Le tableau suivant présente le calcul du coût de revient des produits P1 et P2 sous l’hypothèse que les mêmes frais généraux signifient 10 500 $ relatifs au produit P1 et 10 500 $ relatifs au produit P2.

Le tableau suivant présente le calcul du coût de revient des produits P1 et P2 sous l’hypothèse que les mêmes frais généraux signifient le même montant de frais généraux à l’unité.

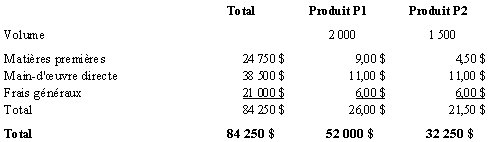
Exercice 3.21

Comme P2 nécessite deux fois plus de kilogrammes par unité que P1, on peut établir l’équivalence suivante :

2 unités de P1 prennent le même temps que 1 unité de P2
2 unités de P1 = 1 unité de P2
2 000 unités de P1 = 1 000 unités de P2
1 000 unités de P1 + 1 000 unités de P2 = 1 000 unités de P1 + 2 000 unités de P1
soit 3 000 unités de P1

Le tableau suivant présente le calcul du coût de revient des produits P1 et P2.

Exercice 3.22

Comme P1 nécessite deux fois plus de temps que P2, on peut établir l’équivalence suivante :

2 unités de P2 prennent le même temps que 1 unité de P1
2 unités de P2 = 1 unité de P1
1 200 unités de P2 = 600 unités de P1
600 unités de P1 + 500 unités de P2 = 1 200 unités de P2 + 500 unités de P2
soit 1 700 unités de P2

Le tableau suivant présente le calcul du coût de revient des produits P1 et P2.

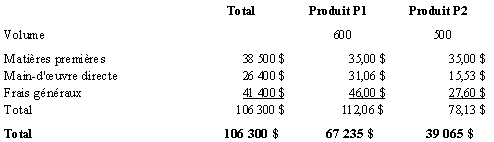
Exercice 3.23

Comme P2 consomme trois fois plus de ressources que P1 dans les deux premiers ateliers, on peut établir l’équivalence suivante :

3 unités de P1 prennent les mêmes ressources que 1 unité de P2
3 unités de P1 = 1 unité de P2
30 000 unités de P1 = 10 000 unités de P2
10 000 unités de P1 + 10 000 unités de P2 = 10 000 unités de P1 + 30 000 unités de P1
soit 40 000 unités de P1

Le tableau suivant présente le calcul du coût de revient de P1 et de P2 dans les deux premiers ateliers seulement.

Pour obtenir le coût de revient de P1, il faut ajouter au coût de ce produit calculé au tableau précédent le coût de ce produit dans le troisième atelier. Le tableau suivant présente le calcul du coût de revient de P1 et de P2 dans les trois ateliers.


 

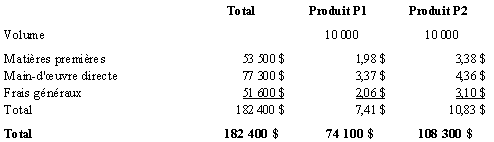
Exercice 3.24

Le tableau suivant indique que le coût de revient du lot du modèle A est de 1 474 500 $ pour un coût de revient unitaire de 49,15 $, alors que celui du lot du modèle B est de 3 392 700 $ pour un coût de revient unitaire de 113,09 $.

Comme une unité du modèle B nécessite deux fois plus de ressources qu’une unité du modèle A pour l’approvisionnement et l’entreposage, on peut établir l’équivalence suivante pour ces deux activités :

2 unités de A = 1 unité de B
60 000 unités de A = 30 000 unités de B
30 000 unités de A + 30 000 unités de B = 30 000 unités de A + 60 000 unités de A
soit 90 000 unités de A

Ainsi, le coût par unité de l’activité d’approvisionnement est de 1,50 $, soit 135 000 $/90 000, et celui de l’entreposage, de 1,04 $, soit 93 600 $/90 000.

Comme une unité du modèle B nécessite 6 kg de matières premières, soit deux fois plus qu’une unité du modèle A qui en requiert 3 kg, on peut établir l’équivalence :

2 unités de A = 1 unité de B
60 000 unités de A = 30 000 unités de B
30 000 unités de A + 30 000 unités de B = 30 000 unités de A + 60 000 unités de A
soit 90 000 unités de A

Ainsi, le coût par unité des matières premières par unité équivalente est de 21 $,
soit 1 890 000 $/90 000.

Comme une unité du modèle B nécessite trois fois plus de temps à l’atelier de moulage qu’une unité du modèle A, on peut établir l’équivalence :

3 unités de A = 1 unité de B
90 000 unités de A = 30 000 unités de B
30 000 unités de A + 30 000 unités de B = 30 000 unités de A + 90 000 unités de A
soit 120 000 unités de A

Ainsi, le coût par unité équivalente de la main-d’œuvre directe à l’atelier de moulage est 15,60 $, soit 1 872 000 $/120 000.

Enfin, nous pouvions déduire les frais de mise en course du lot du modèle B du montant de
6 600 $, relatif à l’activité de mise en course à l’atelier de moulage.

Exercice 3.25

Le tableau suivant permet de répondre à toutes les questions posées dans cet exercice.


 

Nous avons supposé que le coût indirect de fabrication est fixe car rien ne nous indique qu’il est variable, il est donc de 2 040 000 $ peu importe le niveau d’activité.

Selon le scénario a le bénéfice net unitaire est de 32 $. Il est de 17,50 $ selon le scénario b et il est de 22 $ selon le scénario c.

La Société Frigon ltée devrait baisser son prix de vente à 115 $ parce qu’elle réaliserait en moyenne 22 $ par unité sur un volume de 60 000 unités, soit 1 320 000 $ de bénéfice net plutôt que 17,50 $ par unité sur un volume de 48 000 unités, soit 840 000 $. Elle réalisera donc
480 000 $ de plus si elle baisse son prix.

L’arrivée du concurrent lui occasionne un manque à gagner de 600 000 $, soit la différence de bénéfice net entre les scénarios a et c, ou encore de 10 $ pour 60 000 unités, soit l’effet de la baisse du prix de vente.

Exercice 3.26

Le tableau suivant permet de répondre aux deux questions posées dans cet exercice.







Le prix de vente unitaire initialement prévu pour chaque table du lot était de 96 $. Un prix de
102 $ permettrait de réaliser une marge de 20 % sur les 900 unités conformes au niveau de qualité exigé.

Exercice 3.27

D’après le tableau suivant, les coûts prévus sont plus élevés que les coûts engagés pour chacune des trois catégories de ressources. Par rapport aux matières premières, on a surestimé de 1 300 kg la quantité utilisée, l’écart a été réduit par le fait que ces matières ont été payées plus cher que prévu. Par rapport à la main-d’œuvre directe, on a surestimé le taux payé de 2 $, l’écart a été réduit par le fait qu’on a pris un peu plus de temps. C’est au niveau des frais généraux qu’on retrouve l’erreur la plus grande soit de 1 065 $, soit près de 20 % des coûts initialement prévus de cette catégorie.