Chapitre 2
Les coûts et la prise de décision

Objectifs

Après avoir étudié ce chapitre, vous serez capable :

Définir et analyser les coûts dans un contexte de prise de décision

La comptabilité de management vise à produire de l’information financière pour la prise de décision et pour la gestion. Nous proposerons donc des définitions de coûts qui vont nous permettre d’analyser les coûts dans un contexte de prise de décision. Nous illustrerons ces définitions à l’aide d’exemples. Puis, nous vérifierons notre compréhension de ces définitions dans les exercices à la fin de chaque chapitre.

Déterminer les coûts pertinents pour la prise de décision

À l’aide de mises en situation variées, nous sensibilisons le lecteur aux coûts pertinents à la décision.

Analyser certaines décisions influant sur les coûts

Nous traitons 14 exemples dans ce chapitre et nous proposons 24 exercices qui sont liés à des contextes de prise de décision à la fin du chapitre.

Distinguer les coûts fixes des coûts variables

Ces deux notions sont fondamentales à l’analyse coût-volume-bénéfice et à plusieurs modèles comptables tels que la méthode des coûts variables et le budget flexible. Bien les distinguer est utile pour comprendre les limites de ces définitions et de leurs applications.

Appliquer des méthodes permettant de distinguer les coûts fixes des coûts variables

Voir comment la détermination de ces coûts peut mettre en lumière ce qu’ils représentent effectivement; il est donc important de comprendre les hypothèses des méthodes utilisées ainsi que le modèle de comportement sous-jacent à ces méthodes.

Questions de révision

1. En effet, il peut s’agir d’un coût moyen, d’un coût marginal, d’un coût complet de fabrication ou encore d’un coût global incluant une juste portion des frais de vente et d’administration. La seule façon de savoir ce que ce coût représente effectivement est de regarder comment il a été calculé et comment ont été répartis les coûts communs. Prenons une calculatrice de poche qu’on dit coûter 20 $. De quel coût s’agit-t-il? Considère-t-on uniquement le coût de fabrication ou bien inclut-on aussi une juste part des frais de vente et d’administration? Enfin, ce montant inclut-il une juste part des frais de recherche et de développement?

2. Le coût moyen d’un produit est égal au coût total divisé par le nombre d’unités produites, alors que le coût marginal est le coût additionnel associé à la dernière unité produite.

3. C’est la circonstance qui rend un coût pertinent. Un coût est pertinent par rapport à une décision donnée, s’il est susceptible d’être modifié par cette décision.

4. Le coût historique est le coût enregistré au moment de la transaction. Il n’est généralement pas pertinent à une décision donnée. Par ailleurs, il peut servir de point de référence lorsqu’on ne dispose pas de coût actuel ou de valeur au marché.

5. Lorsqu’on doit comparer des coûts à divers points dans le temps, on doit utiliser des coûts actualisés pour que la comparaison ait du sens. En effet, 1 $ aujourd’hui ne vaut pas la même chose que 1 $ dans un an, dans deux ans, etc.

6. Le coût de renonciation est le gain dont on accepte d’être privé en faisant un choix.

7. Le coût de renonciation n’est pas un coût comptable puisqu’il ne résulte d’aucune transaction financière. Donc, aucun principe comptable n’incite à le considérer.

8. Le coût de renonciation est important parce qu’il peut changer la décision. Tout projet, quel que soit le bénéfice qu’il rapporterait, n’est pas acceptable si on doit renoncer à une occasion d’affaires plus avantageuse.

9. Le coût différentiel de deux propositions correspond à la différence entre le coût total de chacune.

10. Le coût variable est directement proportionnel au volume.

11. Le segment significatif est une zone d’activité délimitée par deux volumes; celle-ci correspond habituellement à l’intervalle de volumes d’activité dans lequel opère l’entreprise.

12. Le coût fixe par paliers ne varie pas à l’intérieur d’un même palier mais augmente lorsque certains volumes sont atteints, c’est-à-dire en accédant à un palier plus élevé.

13. Nous pouvons parler de coûts fixes et de coûts variables dans la mesure où à l’intérieur d’un segment significatif l’erreur d’estimation est minimale.

14. Voici des exemples :

a. de coût variable : l’engagement d’un personne à un taux horaire;
b. de coût fixe : les taxes annuelles;
c. de coût fixe par paliers: l’engagement d’un transporteur complémentaire à chaque 1 000 unités livrées;
d. de coût variable par paliers : l’achat de matières où le prix à l’unité est fonction de la quantité achetée;
e. de coût mixte : le coût de l’électricité de l’usine, où le montant est fonction à la fois de la consommation et de la pointe de consommation. 15. Parmi les méthodes intuitives, il y a la méthode de l’ingénierie, l’analyse des comptes et la corrélation individuelle ; il y a la méthode des points extrêmes et ses dérivés ; et il y a la régression linéaire simple et multiple.

16. Dans un premier temps, on détermine la pente b de la droite, qui représente le coût variable unitaire, en divisant la somme correspondant à la variation des coûts par celle qui correspond à la variation observée entre le volume minimal et le volume maximal.

Dans un deuxième temps, on fixe le montant total des coûts variables qui s’appliquent à l’un ou l’autre des points extrêmes en multipliant le coût variable unitaire b par le volume, au point choisi.

On obtient l’ordonnée à l’origine a en calculant la différence entre le montant des coûts variables et le montant des coûts totaux.

17. Pour utiliser la régression linéaire, il faut au préalable disposer de données statistiques en nombre suffisant. Avec moins de 6 couples (x, y) de données dans le cas de la régression simple, on peut tout aussi bien utiliser la méthode des points extrêmes. Le nombre de données nécessaires augmente avec le nombre de variables explicatives que l’on souhaite utiliser.

18. Il y a trois critères. D’abord, l’équation posée comme modèle doit avoir du sens, c’est-à-dire que le facteur représentant la variable x doit expliquer la variable y. Ensuite, les hypothèses du modèle doivent concorder avec la situation étudiée. Enfin, on peut utiliser les informations complémentaires apportées par le coefficient de détermination, les tests statistiques effectués sur les paramètres du modèle et l’estimation par intervalle.

19. La régression tient compte de toutes les données statistiques. De plus, les informations complémentaires apportées par la régression nous informent sur la valeur de la droite estimée, ce que ne peuvent faire les autres méthodes.
  1. Le coefficient r2 indique la fraction de la somme totale des carrés des distances entre la valeur observée et la moyenne, qui est expliquée par la régression. Plus la régression explique, plus cette valeur est près de 1, c’est-à-dire que plus la ou les variables explicatives (x) décrivent le comportement de la variable à expliquer (y), plus cette valeur est près de 1.
21. Le rejet de l’hypothèse nulle, a = 0, n’a d’importance que si la situation étudiée nécessite ce rejet, c’est-à-dire si le modèle prévoit que la droite de régression passe par l’origine. De façon générale, le fait que la droite estimée passe par l’origine n’invalide pas la régression.

22. Rejeter de l’hypothèse nulle, b = 0, équivaut à rejeter l’hypothèse selon laquelle la variable indépendante n’influe pas sur la variable dépendante. En corollaire, accepter cette hypothèse équivaut à nier l’influence de la variable indépendante (x) sur la variable dépendante y.

23. Non, elles établissent des corrélations ou des dépendances entre les variables, mais elles ne permettent pas d’affirmer que l’une influe sur l’autre et non pas l’inverse ou encore que les deux variables ne sont pas déterminées par une troisième variable.

 Exercices

Exercice 2.1

Non, il ne devrait pas.

La variation de coûts entre les deux années est de 212 $, soit 5 412 $ - 5 200 $.

La variation du nombre d’examens repris entre ces deux années est de 16, soit 66 - 50.

Le coût moyen additionnel par examen repris entre ces deux années est donc de 13,25 $, soit
212 $/16.

Selon le modèle du comportement des coûts en coûts fixes et variables, le coût variable total pour 50 unités est de 662,50 $, soit 50 ´ 13,25 $. Du coût total de 5 200 $, on en déduit donc qu’il y a un montant des coûts fixes de 4 537,50 $, soit 5 200 $ - 662,50 $.

La diminution du coût moyen par examen repris, s’explique par la répartition entre un plus grand nombre d’unités du montant de coûts fixes de 4537,50 $.

Exercice 2.2 

Voici le tableau de calculs demandés.
 
Mandats
Coût fixe
Coût variable
Coût marginal
Coût total
Coût moyen
1 000 heures
6 600 $
80 $
80 $
86 600 $
86,60 $
1 100 heures
7 000 $
80 $
480 $
95 000 $
86,36 $
1 200 heures
7 000 $
80 $
80 $
103 000 $
85,83 $

Exercice 2.3

Un coût est pertinent à la décision s’il influe sur le résultat de la décision ou s’il est modifié par celle-ci. Les seuls coûts pertinents sont :

  1. le coût de renonciation associé à la décision de garder les actions, soit 12 % de 10 000 $ pendant un an;
  2. le gain espéré de 6 000 $ dans un an, peut être considéré comme le coût de renonciation associé à la décision de vendre maintenant les actions à 10 000 $.
D’une part, M. Dubois est certain de gagner 1 200 $ dans un an et, d’autre part, il prévoit gagner 6 000 $ avec une probabilité p. M. Dubois devrait attendre si sa conviction (représentée par la probabilité p) lui permet de contrer son aversion pour le risque. (L’analyse de décision tenant compte du critère d’aversion pour le risque dépasse le cadre de ce manuel.)

Si le gain de 6 000 $ était certain (probabilité 1), il recevrait 4 800 $ de plus en gardant les actions encore un an. Le montant de 4 800 $ est un revenu différentiel.

Exercice 2.4

  1. La question du directeur de l’entrepôt n’est pas pertinente, car la valeur comptable, pas plus que le coût d’origine, ne constitue une indication des débours à engager à la suite de l’incendie. La perte réelle pour l’entreprise correspond à la différence entre la valeur de l’entrepôt sur le marché et le montant qu’elle pourra récupérer en assurances.
  2. La question la plus appropriée aux circonstances est la suivante: " Quelle la couverture d’assurances? " et, en second lieu, " Combien nous coûtera la reconstruction de cet entrepôt? "
Exercice 2.5

Le coût de renonciation associé à la décision de transformer un des trois produits au-delà de l’atelier commun est de 120 000 $ par année. Ce montant est le même, que l’on transforme un, deux ou trois produits.

Par ailleurs, dans ce cas, on doit parler de revenu différentiel et de contribution différentielle plutôt que de coût différentiel proprement dit. Voici le tableau des revenus et des coûts liés à cette décision :
 



 


La contribution différentielle doit être comparée avec le coût de renonciation.

Le produit C ne doit pas être transformé au-delà de l’atelier commun, car sa contribution différentielle est négative. Transformer les produits A et B rapporterait au total 20 000 $ de plus, compte tenu du coût de renonciation, soit :
 


60 000 $ + 80 000 $ - 120 000 $


 


Exercice 2.6

Le coût de renonciation associé à cet investissement est le gain auquel cette entreprise renonce en investissant deux millions de dollars, pour ajouter une nouvelle gamme de produits à sa production actuelle plutôt que pour faire un nouvel investissement. Le coût de renonciation que l’entreprise devra subir, si elle ne fait pas cet investissement, est de 240 000 $ par an, soit 12 % de deux millions de dollars.

Exercice 2.7

Le coût de renonciation de Pierre est :

  1. nul au 1er septembre;
  2. de 19 000 $ au 1er novembre, s’il accepte l’offre à 23 000 $; et de 23 000 $ s’il accepte l’offre à 19 000 $;
  3. de 23 000 $ au 15 novembre, s’il accepte l’offre à 26 000 $ et que l’offre de 23 000 $ du 1er novembre est toujours valable; si cette dernière n’était plus valable, son coût de renonciation serait nul;
  4. de 0 $ au 1er février, s’il accepte l’offre de 26 000 $ et que les offres précédentes ne tiennent plus;
  5. de 26 000 $ au 15 février, si l’offre du 1er février est toujours valable.
Exercice 2.8

Le coût de renonciation de M. Caron est :

  1. la somme que serait prêt à payer un acheteur le 14 janvier (elle nous est inconnue);
  2. de 280 000 $ au 15 janvier après avoir pris connaissance de l’offre;
  3. la somme que serait prêt à payer un acheteur le 20 janvier (elle nous est inconnue);
  4. de 315 000 $ au 16 février;
  5. la somme que serait prêt à payer un acheteur au 20 février (elle nous est inconnue).
Exercice 2.9

La réponse à cette question dépend du moment où l’étudiant prend la décision d’étaler son programme de B.A.A. sur quatre années. S’il prend cette décision avant d’entreprendre son baccalauréat, il gagnera 200 $ par semaine huit mois sur douze durant quatre ans tout en faisant son B.A.A. S’il prend cette décision au début de l’été précédant sa troisième année, il gagnera 200 $ par semaine huit mois sur douze durant deux ans.

Première solution: il prend sa décision avant d’entreprendre son B.A.A.

Dans ce cas, il gagnera 6 933 $ pour huit mois de travail sur douze, soit 52 ´ 8/12 ´ 200 $ pendant quatre ans, plus, le troisième été, un montant de 3 000 $, qu’il ne gagnerait pas par ailleurs. Le coût de renonciation, s’il opte pour un B.A.A. en trois ans, est donc de 30 733 $, soit 4 ´ 6 933 $ + 3 000 $.

Par ailleurs, s’il opte pour un B.A.A. en quatre ans, son coût de renonciation est de 24 000 $, soit le salaire qu’il gagnerait à la fin de ses études.

Le revenu différentiel associé au B.A.A. en quatre ans est donc de 6 733 $, soit 30 733 $ -
24 000 $.

Deuxième solution: il prend sa décision avant l’été de sa troisième année de B.A.A.

Dans ce cas, il gagnera 6 933 $ pour neuf mois de travail sur douze, soit 52 ´ 8/12 ´ 200 $ pendant deux ans, plus, le troisième été, un montant de 3 000 $, qu’il ne gagnerait pas par ailleurs. Le coût de renonciation, s’il opte pour un B.A.A. en trois ans, est donc 16 867 $,
soit 2 ´ 6 733 $ + 3 000 $.

Par ailleurs, s’il opte pour un B.A.A. en quatre ans, son coût de renonciation est de 24 000 $, soit le salaire qu’il gagnerait à la fin de ses études.

Le revenu différentiel associé au B.A.A. en trois ans est donc de 7 133 $,
soit 24 000 $ - 16 867 $.

Exercice 2.10

1. Si le second éditeur ne publie pas un ouvrage sur le même thème, le coût de renonciation est de 50 % de 5 % de 200 000 $, soit 5 000 $. Le coût de renonciation pourrait être plus élevé si on estime qu’il pourrait rester avec un stock de l’ancien manuel.

2. En prenant pour hypothèse que le second éditeur publie un ouvrage sur le même thème, on obtiendra un coût de renonciation nul.

 Exercice 2.11

Voici les graphiques qui correspondent le mieux aux dix situations décrites :

  1. le graphique b;
  2. le graphique f;
  3. le graphique e;
  4. le graphique j;
  5. le graphique g;
  6. le graphique h;
  7. le graphique b;
  8. le graphique d;
  9. le graphique i;
  10. le graphique k.
Exercice 2.12

Si nous posons l’hypothèse que tous les coûts de l’entreprise sont soit fixes, soit variables, nous pouvons tracer une droite entre ces deux points et expliquer l’augmentation des coûts par l’augmentation du niveau d’activité.

Le coût variable unitaire est égal à: 26 000 $ - 20 000 $
                                                     21 000 h - 13 000 h

soit 0,75 $ l’heure.

Le coût fixe mensuel est égal à 10 250 $, soit (20 000 $ - 13 000 ´ 0,75 $).

Exercice 2.13

1. Le volume d’activité mensuel, situé entre 70 000 et 80 000 unités, correspond au segment significatif. Les statistiques observées se situent dans cet intervalle et les résultats des analyses ne sont valables que dans cet intervalle. Nous ne pouvons les extrapoler qu’en posant des hypothèses de comportement relativement restrictives.

2. Voici un graphique des coûts fixes et variables par unité :

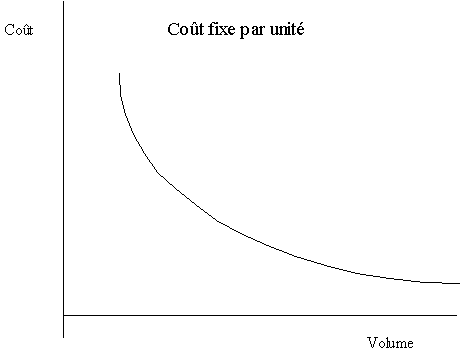
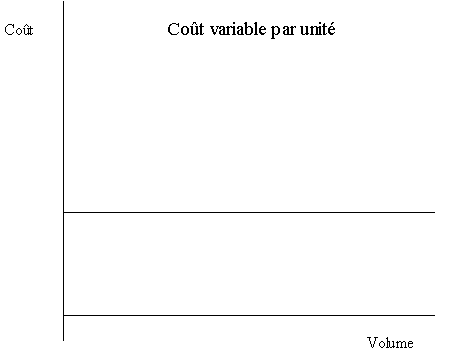
La courbe des coûts variables par unité se présente comme une droite parallèle à la droite des abscisses car ces derniers sont constants. La courbe des coûts fixes par unité décroît lorsque le volume d’activité s’accroît, car le montant total des coûts fixes demeure le même soit 200 000 $ par mois.

3. Le coût total pour un volume d’activité de 100 000 unités est de :

Coûts fixes:         200 000 $
Coûts variables:  250 000 $
Total:                450 000 $ Cependant, puisque que le volume de 100 000 unités est situé à l’extérieur du segment significatif de 70 000 à 80 000 unités, il faut ajouter les deux conditions restrictives suivantes : Ces deux conditions ne se réaliseront que s’il n’y a aucun coût fixe par palier, variable par palier ou mixte.

4. Le montant des coûts fixes est toujours de 200 000 $, à moins qu’on ne pose une autre hypothèse. Ce montant représente au niveau de 40 000 unités, 66,67 % du coût total alors qu’il était de 50 % du coût total au niveau de 80 000 unités.

 Exercice 2.14

Les coûts de 0,36 $ et 0,48 $ sont des coûts unitaires complets, c’est-à-dire qu’on les a obtenus en additionnant les coûts fixes et les coûts variables, puis en divisant cette somme par le nombre total de kilomètres parcourus. En effet,
 


 
Kilomètres
parcourus
Coût
total
Moyenne
par km
Cette année
25 000
12 000 $
0,48 $
L’année précédente
40 000
14 400 $
0,36 $

Si l’on pose que tous les coûts sont strictement fixes ou strictement variables, on peut établir l’équation d’une droite. Selon les statistiques du tableau précédent, le coût variable unitaire est de 0,16 $ le kilomètre, soit une variation de 2 400 $ pour une variation de 15 000 kilomètres. On peut ensuite établir le montant des coûts fixes à 8 000 $, soit (12 000 $ - 25 000 ´ 0,16 $). Le coût moyen par kilomètre parcouru passe de 0,36 $ à 0,48 $ parce que le montant de 8 000 $ est réparti sur 25 000 km comparativement à 40 000 km l’année précédente. 

Exercice 2.15

1. La variation de coût entre ces deux années est de 4 597 540 $.
La variation du nombre de jours-patients entre ces deux années est de 7 300.
Le coût moyen additionnel par jour-patient entre ces deux années est donc de 629,80 $.

2. Nous sommes forcés de répondre non à la deuxième partie de la question car si tel était le cas, le coût variable par jour-patient serait de 629,80 $, ce qui n’a aucun sens. Un tel taux nous donnerait un coût fixe négatif. En effet, 285 430 jours-patients à 629,80 $ donnent 179 763 814 $, soit plus que le coût total de 92 795 410 $.

À noter aussi que le nombre de jours-patients diminue de 2 920 jours entre les années 1994 et 1996, tandis que le coût augmente de 3 509 110 $. Cela nous amène à conclure que les coûts des soins de santé dans cet établissement ne varient pas selon le nombre de jours-patients.

 Exercice 2.16 1. La variation des dépenses entre les deux cycles 1991-1992 et 1992-1993 est de 1 654 400 $.
La variation du nombre d’EÉÉTP entre ces deux cycles est de 36,72.
La dépense moyenne additionnelle par EÉÉTP entre ces deux cycles est donc de
45 054 $.

2. Non, car si tel était le cas, le coût variable par EÉÉTP serait de 45 054 $, ce qui n’a aucun sens. Un tel coût par unité nous donnerait un coût fixe négatif puisque le coût variable serait de 232 724 184 $, soit (5 165,45 ´ 45 054 $).

Remarquez que le nombre d’EÉÉTP diminue de 3,18 unités entre les cycles 1990-1991 et 1992-1993, tandis que le coût augmente. Cela nous amène à conclure que les dépenses d’enseignement à l’École des HEC ne varient pas en fonction du nombre d’EÉÉTP.

 Exercice 2.17

La variation de coûts entre les deux années est de 199 900 $.
La variation du nombre d’unités défectueuses entre ces deux années est de 30.
Le coût moyen additionnel par unité défectueuse entre ces deux années est donc de 6 663 $.
Selon le modèle du comportement des coûts en coûts fixes et variables, le coût variable total pour 100 unités est de 666 333 $, ce qui donne des coûts fixes de 333 667 $. 

La diminution du coût moyen par unité vient de la répartition sur un plus grand nombre d’unités, soit 130 plutôt que 100, du montant de coûts fixes de 333 667 $.

L’entreprise n’a donc pas intérêt à augmenter le nombre d’unités défectueuses.

Exercice 2.18

1. La variation de coût entre les deux points extrêmes est la même pour les deux consultants, soit une variation de 5 000 000 $ entre les coûts des mois de janvier et d’avril.
La variation du nombre de mandats entre les deux points extrêmes est également la même, soit de 1 000 mandats.
Le coût moyen additionnel par mandat entre les deux points extrêmes est donc de 5 000 $.
Selon le modèle des coûts en coûts fixes et variables, le coût variable total pour 2 000 mandats est de 10 000 000 $, ce qui donne des coûts fixes de 2 000 000 $ pour les deux consultants.

2. Le consultant A présenterait le coefficient de détermination le plus élevé, parce que les observations des mois de février et de mars sont beaucoup plus près l’une de l’autre que celles des mêmes mois pour le consultant B.

 Exercice 2.19 1. La variation de coûts entre les deux points extrêmes est la même pour les deux entreprises, soit une variation de 350 $ entre les frais généraux relatifs à janvier et à avril.
La variation du nombre d’unités entre les deux points extrêmes est également la même, soit de 50 unités.
Le coût moyen additionnel par unité entre les deux points extrêmes est donc de 7 $.
Selon le modèle des coûts en coûts fixes et variables, le coût variable total pour 100 unités est de 700 $, ce qui donne des coûts fixes de 100 $.

2. La deuxième entreprise présenterait le coefficient de détermination le plus élevé parce que les observations des mois de février et de mars sont beaucoup plus près l’une de l’autre que celles des mêmes mois pour l’entreprise B.

 Exercice 2.20 1. Pour décrire le volume d’activité à l’aide du montant des ventes, il y a deux points extrêmes de volume minimal, soit les mois de juillet et d’août à 56 000 $ de ventes, et un point extrême de volume maximal, soit le mois de décembre à 84 000 $ de ventes. Il est rare qu’une telle situation ( deux points extrêmes à une extrémité ) se produise; cependant il faut la prévoir. Utilisons l’observation du mois de juillet, car le montant des frais de déplacement est plus faible mais ce n’est pas nécessairement la règle.

Le coût variable unitaire des frais de déplacement en fonction des dollars de ventes est donc de 0,125 $ par dollar de vente, soit une variation de 350 $ des frais de déplacement, soit 1 120 $ - 770 $, pour une variation de 28 000 $ de ventes.

Le montant des frais fixes liés au déplacement est de 70 $,
soit 770 $ - 56 000 $ ´ 0,0125 $.  

2. Selon la méthode de la régression linéaire, nous obtenons les résultats suivants :

y = 104,22 + 0,011642x

  À l’aide de la fonction REGR du logiciel EXCEL de Microsoft, nous avons obtenu les résultats suivants :

seb = 0,0118669                       sea = 83,64268417
r2 = 0,905880747                     sey = 33,89863783
F = 96,24818701                     Dl = 10
ssrég = 122 091,6667               ssrésid = 11 491,17647

  3. Selon l’équation de la droite obtenue par la méthode des points extrêmes, nous estimons les frais de déplacement à 1 170 $, soit 70 $ + 88 000 $ ´ 0,0125 $.

Selon l’équation de la droite obtenue par la régression linéaire, nous estimons les frais de déplacement à 1 128,73 $, soit 104,22 $ + 88 000 $ ´ 0,011642 $.

4. La méthode de la régression linéaire apporte des informations sur la valeur de la droite estimée que la méthode des points extrêmes n’apporte pas. Nous savons notamment que r2 = 0,905880747; la régression explique donc 90 % des écarts par rapport à la moyenne; ce qui est excellent.

 Exercice 2.21 1. Selon la méthode des points extrêmes :
y = 520 000 $ + 2,50 $ ´ ( heures de MOD )

Selon la méthode de la régression linéaire :
y = 498 781,37 $ + 3,0556 $ ´ ( heures de MOD )

2. Selon la méthode des points extrêmes :
y = 519 240,53 $ + 0,3164556 $ ´ ( coût de MOD )

Selon la méthode de la régression linéaire :
y = 497 491,75 $ + 0,388566483 $ ´ (Coût de MOD)

3. En premier lieu, il y a le coefficient r2. Dans le cas de la régression en fonction des heures de MOD, il est égal à 0,7936; et, dans le cas de la régression en fonction du coût de la MOD, il est égal à 0,806. On peut dire, dans un cas comme dans l’autre, que la régression explique environ 80 % du carré des écarts entre les valeurs observées et la moyenne des frais généraux, ce qui est excellent.

Nous pourrions également produire un intervalle de confiance de la valeur moyenne et un intervalle de prévisibilité d’une observation.

4. On ne peut faire une telle régression car les deux variables explicatives envisagées, soit les heures de MOD et le coût de la MOD, ne sont pas indépendantes l’une de l’autre (multicolinéarité). En effet, le coût de la MOD est égal aux heures de MOD multipliées par un taux horaire.

 Exercice 2.22 1. Elle devrait prendre en compte la disponibilité des données et l’utilité du modèle. À première vue, le choix du nombre de dessins semble préférable parce que le nombre d’heures est fonction du nombre de dessins. Il est préférable, lorsque les données sont disponibles de choisir la cause d’origine. Or le nombre de dessins à exécuter est certainement un facteur déterminant du travail à faire.

2. Selon la méthode des points extrêmes :
y = 5 078 $ + 11,731 $ ´ ( heures totales )

Selon la régression linéaire simple :
y = 15 820,64 $ + 11,41472875 $ ´ ( heures totales )

3. Selon la méthode des points extrêmes :
y = 2 570 $ + 2 502,7517 $ ´ ( nombre de dessins )

Selon la régression linéaire simple :
y = - 16169,63 $ + 2 386,695 $ ´ ( nombre de dessins )

 Exercice 2.23 1. Voici les données :
 
Kilomètres
parcourus
Coût
total
Moyenne
par kilomètre
Première année
42 000 000
12 432 000 $
0,296 $
Dernière année
24 000 000
9 552 000 $
0,398 $
Différence
18 000 000
2 880 000 $
0,160 $

  Selon les statistiques du tableau précédent, le coût variable unitaire est de 0,16 $ par kilomètre parcouru, obtenu en prenant le ratio (variation des coûts/variation du nombre de kilomètres), soit 2 880 000 $/18 000 000 km. On peut établir les coûts fixes à
5 712 000 $, soit 12 432 000 $ - 42 000 000 ´ 0,16 $. Si la moyenne est plus élevée la deuxième année, c’est que les coûts fixes de 5 712 000 $ ont été répartis sur seulement
24 000 000 de kilomètres au lieu de 42 000 000 de kilomètres comme l’année précédente.

2. il y a cohérence parfaite entre le résultat de la régression linéaire et le résultat précédent puisque le chiffre de 0,1583 $ le kilomètre parcouru comme coût variable unitaire au cours de l’année est très près de 0,16 $ le kilomètre parcouru, obtenu avec la méthode des points extrêmes. De plus, l’ordonnée à l’origine de 480 142 $, obtenue à partir de données mensuelles, équivaut à 5 761 704 $, soit 12 ´ 480 142 $, si l’on avait eu des données annuelles; ce montant est également très près de 5 712 000 $. Il n’y a donc aucune incohérence entre les deux résultats.

Enfin, les statistiques r2 = 0,9123 et tb = 5,624 sont tout à fait significatives. Le r2 indique que la variable explicative ou indépendante, soit le nombre de kilomètres, explique dans une proportion de 91 % la somme des carrés des écarts des observations à la droite de la régression estimée, donc explique le comportement de la variable dépendante, soit le coût. Enfin, la variable tb nous permet de rejeter sans crainte d’erreur l’hypothèse, nulle, à savoir que la variable indépendante n’explique rien. Rejeter cette hypothèse équivaut à accepter par défaut qu’elle explique le comportement de la variable dépendante.

3. Comme la distance maximale parcourue serait de 25 000 000 de kilomètres, le montant maximal de revenus de location est de 5 000 000 $, soit 25 000 000 ´ 0,20 $, inférieur de 712 000 $ au montant des coûts fixes établis soit 5 712 000 $.

Par ailleurs, si nous utilisons le montant de 480 142 $ de coûts fixes par mois, estimé par la régression, nous devons le multiplier par 12 puisqu’il s’agit d’un montant mensuel. Le montant des coûts fixes annuels est donc de 5 761 704 $, ce qui est de 761 704 $ supérieur au montant de 5 000 000 $, de revenus de location estimé. Donc, le déficit minimal est de 712 000 $, mais il pourrait être de 761 704 $.

 Exercice 2.24 1. Les deux points extrêmes sont les données venant de l’Université du Québec et de l’Université Bishop’s.
Établissement EÉÉTP Coût
Université du Québec 47 433 607 660 655 $
Université Bishop’s 2 128 19 985 666 $
Différence 45 305 587 674 989 $
La pente de la droite sera donc de 12 971,41 $, soit 587 674 989  $/45 305 EÉÉTP.
L’ordonnée à l’origine sera de - 7 611 018,17 $, soit 587 674 989 $ - 45 305 ´ 12 971,41 $.

2. Le coefficient de détermination r2 de la droite de régression est très élevé à 0,94, ce qui signifie une corrélation très forte entre le nombre d’EÉÉTP et le coût total d’un établissement universitaire. Cependant, cela n’implique pas nécessairement une relation de cause à effet.

Rappelons les conditions qui peuvent causer une corrélation élevée :

 Ce problème indique bien que les coûts ne sont pas fonction du nombre d’EÉÉTP. Cependant, les budgets, eux, sont fonction, en partie du moins, du nombre d’EÉÉTP et les coûts sont contrôlés, c’est-à-dire surveillés et limités en fonction des budgets disponibles.

3. Je n’utiliserais pas cette équation pour les raisons suivantes :

  Les coûts des établissements universitaires ne varient pas en fonction du nombre d’étudiants, mais plutôt en fonction des budgets disponibles.

Selon le premier argument, celui des membres favorables à l’augmentation des droits, l’évidence statistique démontre que les coûts ne varient pas en fonction du nombre d’EÉÉTP. Il suffit d’essayer une prévision, et les résultats ne sont pas très précis pour les établissements qui ont relativement peu d’EÉÉTP. Par exemple dans le cas de l’École des HEC :

y = 12 146 728,08 $ + 13 769,09 $ ´ 4 937 EÉÉTP
soit y = 80 188 590,12 $
alors que le coût total est de 49 956 525 $.

4. Le premier argument :
Certains frais fixes spécifiques à un programme ne sont pas soumis au modèle de régression utilisé. L’argument est fondé sur un coût marginal par EÉÉTP. Or, le coût marginal par EÉÉTP est nul à toutes fins pratiques car un étudiant de plus ou de moins ne change rien au coût, une fois le programme lancé.

Le deuxième argument :
Cet argument est valable. Cependant, il laisse de côté tous les autres coûts associés au programme, notamment la mise en marché, l’activité au bureau du registraire, aux services financiers ainsi que les coûts de la gestion des programmes et les coûts du logement. 

5. Le premier argument:
Ce premier argument est tout à fait valable. Il s’agit d’une comptabilité par activités. Cependant, on ne peut pas conclure qu’il faille augmenter les droits de scolarité car nous ne connaissons pas les coûts de ces activités.

Le deuxième argument:
Le calcul effectué donne une approximation assez grossière du coût. Cependant, la logique est respectée. La seule façon d’obtenir une estimation plus précise serait de recouvrir à une comptabilité par activités.

6. Une proposition:
D’une part, utiliser une comptabilité par activités touchant les coûts spécifiques à tous les programmes d’enseignement. Cette comptabilité nous permettrait d’établir avec précision les coûts spécifiques à chacun des programmes d’enseignement.

D’autre part, imputer un montant à chacun des programmes pour couvrir tous les coûts communs aux programmes pour lesquels nous n’avons pas jugé bon de faire une comptabilité par activités. 

Deux arguments en faveur :

 Une limite à la proposition:
Les coûts communs comprenant la bibliothèque, l’informatique, l’audiovisuel, les laboratoires ainsi que la direction de l’École, étant sensiblement importants, le taux d’imputation risque d’être, lui aussi, relativement important.