Chapitre 2 : Processus stochastiques stationnaires

1. Les séries chronologiques comme réalisation d'un processus stochastique

2. Rappel

3. Processus stochastique stationnaire : la série idéale

4. Processus multivarié

5. Estimation des paramètres caractérisant un processus stationnaire

6. Interprétation

7. Test de Ljung-Box : comment détecter une série bruit blanc?

Programmes : CORR.PRG et FAMA.PRG

1. Les séries chronologiques comme réalisation d'un processus stochastique

On peut considérer chaque observation d’une série chronologique comme la réalisation d’une variable aléatoire : par exemple, y_90 :3 est la réalisation de la variable aléatoire Y_90 :3. Par malchance, il y a eu la guerre du Golfe et le PIB américain a été influencé négativement. On aurait pu ne pas avoir de guerre et le PIB aurait alors évolué d’une autre façon. En fait, une multitude de facteurs qui se réalisent ou non conditionnent l’évolution du PIB (ex. Est-ce que Greenspan est de bonne humeur?).

De la même façon, y_90 :4 est la réalisation d’une autre variable aléatoire Y_90 :4.

La particularité d’une série chronologique est qu’il existe fort probablement des liens entre les deux variables aléatoires sous-jacentes, i.e. Y_90 :3 et Y_90 :4. C’est là toute la difficulté.

2. Rappel

Supposons une variable aléatoire Y₁. On la caractérise habituellement par deux paramètres :

i. moyenne m₁ = E(Y₁) mesure de localisation

ii. variance Var(Y₁) = E (Y₁-m₁) (Y₁-m₁) = g₁ mesure de dispersion

La variance g₁ est nécessairement positive. Dans le cas de deux variables aléatoires, on étudiera les propriétés du vecteur (2x1)

Y =

EY = =m (2x1)

VarY = E(Y-m) (Y-m)’ = G (2x2)

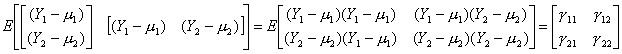
g₁₁ et g₂₂ correspondent respectivement aux variances de Y₁ et Y₂. g₁₂ est la covariance entre Y₁ et Y₂ : elle peut être positive ou négative. Par définition, g₁₂ = g₂₁, i.e. la covariance entre Y₁ et Y₂ est la même que la covariance entre Y₂ et Y₁ : de façon plus mathématique, la matrice G est symétrique, i.e. G= G’ (en fait G est une matrice symétrique définie positive, une condition un peut similaire au fait que les variances soient positives).

Dans le cas plus général de T variables aléatoires Y_t t=1, ... T représentées sous forme matricielle par le vecteur (Tx1) Y’ = [ Y₁ Y₂ ... Y_T], nous avons

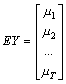(Tx1)

Var Y = (TxT)

Cette distribution multidimensionnelle est caractérisée par T moyennes et (½)(T)(T+1) variances et covariances, un nombre de paramètres difficile à estimer avec ... seulement T observations. Il faut absolument simplifier!

3. Processus stochastique stationnaire : la série idéale

Reprenons le problème d’une autre façon, voici ci-dessous le graphique d’une série «idéale» très stylisée:

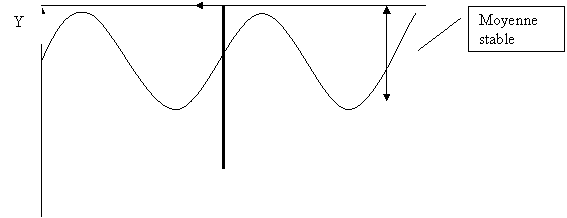
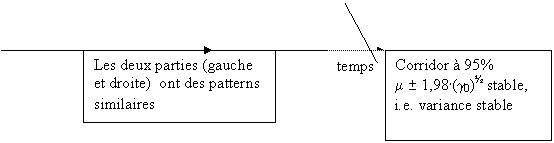
Elle a fondamentalement trois caractéristiques :

i. elle oscille autour d’une moyenne fixe qui ne dépend pas du temps ;

ii. elle est contenue dans des bornes fixes (variance) qui sont fixes à travers le temps;

iii. si on coupe la série en deux, les parties de gauche et de droite ont des comportements similaires (covariance ne dépend pas du temps).

Un processus stochastique est dit stationnaire d’ordre deux si les deux premiers moments de la distribution conjointe ne dépendent pas du temps.

(Note : pour simplifier la notation, on laisse tomber la distinction entre Y, la variable aléatoire, et y une réalisation. Dans certains cas y, représentera la variable aléatoire; dans d’autres cas, y sera associé à une réalisation. Dans la plupart des cas, la distinction ne posera pas de problèmes.)

En résumé, dans le cas d’une série stationnaire y_t (t=1,2,...,T)

· E(y_t) = m pour tout t.

· Var(y_t) = E(y_t- m)² = g₀ pour tout t

· Cov(y_t y_t-j) = E(y_t- m)(y_t-j- m) = g_j j=1,2,3 ...

· Corr(y_t y_t-j) = (g_j/g₀) = r_j j=1,2,3 avec r₀=1.

La moyenne ne dépend pas du temps. La variance ne dépend pas du temps. Les auto-covariances g_j ne dépendent pas du temps mais seulement du délai entre y_t et y_t-j. Les auto-corrélations ne dépendent pas du temps.

Sous forme, un peu différente :

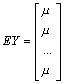(Tx1)

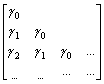Var Y = (TxT)

4. Processus multivarié

Dans le cas d’un processus multivarié stationnaire qui comprend k variables, on notera

y_t’ = [y_1t y_2t ... y_kt] et

E(y_t) = m (kx1)

Cov(y_t y_t-j) = E (y_t-m)(y_t-j-m)’ = G_j (kxk)

Dans le cas simple où k=2 et m=0, on a

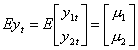
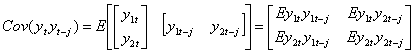
Reprenons chaque morceau séparément :

E y_1t y_1t-j = g₁₁(j) = g₁₁(-j) Auto-covariance de la première variable avec elle-même!

E y_2t y_2t-j = g₂₂(j) = g₂₂(-j) Auto-covariance de la deuxième variable avec elle-même!

E y_1t y_2t-j = g₁₂(j) ¹ g₁₂(-j) Covariance croisée de la première avec la deuxième retardée.

E y_2t y_1t-j = g₂₁(j) = g₁₂(-j) Covariance croisée de la deuxième avec la première retardée.

Voir graphique en classe.

5. Estimation des paramètres caractérisant un processus stationnaire

Moyenne

i=1,...,k (k variables)

Variance -covariance

Auto-covariance croisée entre la variable i et la variable s avec un délai de j.

Corrélation

Sous l’hypothèse nulle H₀ que les séries y_it sont bruit blanc (aucune corrélation, mouvements purement erratiques),

.

Conséquemment, il est possible de faire le test suivant :

H₀ : le coefficient r_is(j) = 0

H₁ : le coefficient r_is(j) ¹ 0

à l’aide de la statistique usuelle

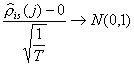
Note : RATS calcule les écarts-types de façon légèrement différente. Voir instruction CORRELATE dans le manuel.

6. Interprétation

Se référer à la discussion en classe.

7. Test de Ljung-Box : comment détecter une série bruit blanc?

Une série bruit blanc est caractérisée par un comportement erratique avec absence de corrélation entre les périodes adjacentes. Il s’agit d’une série de référence fondamentale pour plusieurs raisons : i. au minimum, un phénomène à modéliser ne doit pas être bruit blanc puisqu’il n’y a rien à faire avec une telle série! ii. dans certains cas (résidus de régression), la propriété bruit est désirable et même une condition exigée.

Pour tester si une série est bruit blanc, deux approches sont possibles. Dans un premier cas, on peut tester individuellement chaque coefficient d’auto-corrélation ... ce qui peut être long, fastidieux et même contradictoire. Quoi faire quand on ne peut rejeter l’hypothèse de nullité pour tous les coefficients sauf un? On adopte habituellement l’autre approche qui propose un test global pour évaluer la nullité de tous les coefficients simultanément. Box et Pierce et ensuite Ljung et Box ont développé un test à cet effet qu’on appelle aussi test porte-manteau. Ce test repose sur le théorème bien connu suivant :

Théorème : La somme de J variables aléatoires normales indépendantes centrées réduites au carré suit une distribution X² avec J degrés de liberté.

Supposons que nous nous cherchons à vérifier si la série y_t est bruit blanc.

H₀ : r_i = 0 i=1,...,J

H₁ : r_i ¹ 0 i=1,...,J

On sait que

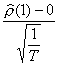suit une N(0,1)

tout comme

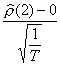suit une N(0,1).

Alors, en utilisant le théorème, on peut montrer que

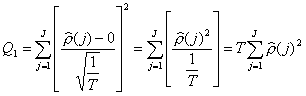
Q₁ ou le test de Box Pierce correspond tout simplement à T fois la somme des auto-corrélations au carré de la série y. Q₁ suit une X²(J). L’intuition est intéressante : si les sont petits, la corrélation entre périodes adjacentes est faible. Les seront aussi petits et la somme Q₁ aussi. Conséquemment, la valeur de Q₁ calculée sera plus petite que la valeur critique du X²(J) et on ne pourra pas rejeter H₀.

Ljung et Box ont montré que le test

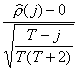suivait de façon encore plus étroite une N(0,1).

Le test Q₂

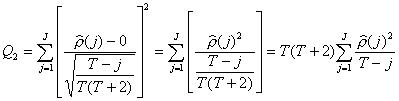
offre donc une meilleure performance et est maintenant utilisé de façon routinière dans tous les logiciels statistiques dont RATS bien sûr.