Chapitre 1 : Description des séries chronologiques

1. Pourquoi étudier les séries chronologiques?

2. Portefeuille de séries chronologiques : flux, stock, fréquence, etc.

3. Caractéristiques des séries et transformations usuelles

4. Saisonnalité et désaisonnalisation

Annexe : Transformation logarithmique et taux de croissance

Programme : trimes.prg

1. Pourquoi étudier les séries chronologiques?

De façon détournée, les séries chronologiques font partie de notre quotidien. Par exemple, le journal télévisé rapporte tous les jours la valeur du TSE300 ou du taux de change du dollar canadien. On fait même de magnifiques graphiques dans nos quotidiens. Au-delà de l’information véhiculée, il faut chercher à modéliser les mécanismes sous-jacents pour éventuellement mieux comprendre la variable en question et ... qui sait, mieux la prévoir!

Définition : Une série chronologique est une suite ordonnée d’observations notée y_t , t=1,...T.

2. Portefeuille de séries chronologiques : flux, stock, fréquence, etc.

Les graphiques joints illustrent toutes sortes de séries chronologiques. On peut les représenter à l’aide du tableau suivant :

Données	Flux : mesuré au cours de la période	Stock : mesuré à un moment précis de la période (photographie)	Prix : mesuré à un moment précis
Quinquennales
Annuelles
Trimestrielles	GDP US (PIB)
Mensuelles		Taux de chômage	IPC
Hebdomadaires			Taux d’intérêt
Quotidiennes			SP500

· Idéalement, on devrait utiliser les séries sous leur fréquence naturelle;

· En pratique, on procède à des conversions des données d’une fréquence à une autre (ex. mensuel vers trimestriel);

· Il faut exercer une grande prudence dans les méthodes de conversion et les relations qu’on établira par la suite entre plusieurs variables (ex. calcul du taux d’intérêt réel ex post);

3. Caractéristiques des séries et transformations usuelles

transformation logarithmique

Notons tout d’abord que dans la grande majorité des cas, la transformation logarithmique est très utile : i. la pente de la série transformée correspond au taux de croissance ; ii. la première différence de la série est plus stable et iii. la différence entre deux séries s’interprète aussi comme une distance en pourcentages. En fait, la transformation logarithmique (en pratique ln) nous libère des unités de mesure et introduit des unités de pourcentage qui sont relatives, une caractéristique bien utile quand les données couvrent de longues périodes. Voir les graphiques en niveau et en log dans le programme TRIMES.PRG.

trois transformations usuelles

Les séries chronologiques sont rarement utilisées comme telles dans des travaux économétriques. Pour toutes sortes de raisons qui seront étudiées durant le cours, on applique essentiellement trois types de transformation (en plus de la transformation logarithmique) :

i. on estime une tendance qui est ensuite retranchée de la série : la résultante est une série en déviations par rapport à sa tendance;

ii. on prend la première différence de la série;

iii. dans le cas de deux séries, on s’intéresse à la différence entre les deux séries.

Idéalement, les séries finales (après transformation) obtenues devraient avoir un comportement plus «stable».

tendance linéaire

Pour trouver un estimé de la pente i.e. le taux de croissance instantané d’une série, on estime la régression suivante :

log y_t = a + b t + u_t où t=1,2,..., T

	Variable dépendante	Variables indépendantes
Période	ln yt	constante	T
1991 :1	ln y1991 :1	1	1
1991 :2	ln y1992 :2	1	2
...	..	...	...
1993 :4	ln y1993 :4	1	12

L’échelle de la variable t n’est pas importante en autant que t augmente de façon régulière. L’estimé de b, la pente de la droite de régression, correspond au taux de croissance instantané de y_t et s’avère ainsi une approximation du taux de croissance discret (y_t-y_t-1)/y_t-1.

La valeur prédite est donnée par a* +b*t où le symbole * indique un estimé (i.e. a* = â des livres d’économétrie). Celle valeur prédite correspond à la partie tendancielle de ln y_t i.e. le potentiel en macroéconomie. Les résidus estimés, ln y_t - a* +b*t, correspondent à la partie cyclique, c’est-à-dire la déviation en pourcentage de ln y_t par rapport au potentiel (le GAP en macroéconomie).

tendance linéaire avec brisure

Dans bien des cas, la série n’a pas de tendance stable et des points de rupture sont observés. Ainsi, supposons que le taux de croissance de la série (la pente) change à partir d’un point donné t₀. Comment estimer ce nouveau modèle qui devrait inclure deux tendances : une avant et une après!

Supposons une rupture à la période t₀, le modèle suivant permet de capter les deux tendances :

ln y_t = a + bt + b₁(t-t₀)D_t

où D_t = 1 si t>t₀ et 0 autrement .

Si t est plus petit ou égal à t₀ alors D_t = 0 et

ln y_t = a + bt (comme avant).

Si t > t₀ alors

ln y_t = a+bt +b₁(t-t₀)

= (a-b₁t₀) + (b+b₁) t

La nouvelle pente ou taux de croissance après la rupture t₀ est égale à b+b₁. Supposons la rupture à la période 1992 :3, i.e. t₀=7, alors

	Variable dépendante	Variables indépendantes
Période	ln y	constante	t	(t-t0)Dt
1991 :1	ln y1991 :1	1	1	(1-7)0=0
1991 :2	ln y992 :2	1	2	(2-7)0=0
...	..	...	...	...
1992 :2		1	6	(6-7)0=0
1992 :3		1	7	(7-7)0=0
1992 :4		1	8	(8-7)1=1
				(8-7)1=2
...	...	...	...	...
1993 :4	ln y1993 :4	1	12	(12-7)1=5

On voit bien ici que nous avons deux tendances : la première [1,2,3,4 ...]débute à la période 1991 :1. La deuxième [1,2,3 ...] débute à la période 1992 :4.

tendance lisse : hodrick-prescott

Poussé à l’extrême, on pourrait imaginer une situation où la tendance (la pente de la valeur prédite) change souvent, à la limite continuellement. Ainsi, toute série serait composée de deux éléments :

ln y_t = composante tendancielle + composante cyclique

ln y = t_t + (ln y_t - t_t )

Au lieu de supposer que t_t suit un modèle linéaire en t, on peut supposer comme les actuaires que t_t change continuellement à une vitesse donnée par le coefficient l. Conséquemment, on pourra «estimer» t_t en minimisant le critère suivant (voir aussi RATS 5.0, UG, p. 376):

La première partie de la formule représente les déviations de la série par rapport à la tendance : plus les déviations sont grandes, plus le critère augmente. La deuxième partie correspond au changement des changements, i.e. la dérivée seconde. Ainsi, il y a trois possibilités intéressantes :

· l = très grand. On pénalise fortement la dérivée seconde. Pour minimiser le critère, on gardera la dérivée seconde à zéro, donc la pente (dérivée première) sera fixe. Ceci correspond au cas linéaire.

· l = 0. Aucune pénalité pour la dérivée seconde qui pourra varier de façon importante. La tendance sera égale à la valeur de la série observée, i.e. ln y_t = t_t .

· l = 1600. cas intermédiaire choisi par Kydland et Prescott (1990).

Une fois la tendance estimée, on peut trouver la portion cyclique de façon usuelle.

la premièrre différence

À la recherche d’une certaine «stabilité», on peut aussi transformer notre série initiale en prenant la première différence

D ln y_t = ln y_t – ln y_t-1 =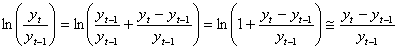

La première différence du log d’une série est en fait une approximation de son taux de croissance discret.

Pour estimer la moyenne du taux de croissance, on peut estimer la régression suivante :

D ln y_t = a + u_t

où a représente le taux de croissance moyen.

	Variable dépendante	Variable indépendante
Période	Dln yt	constante
1991 :2	Dln y1991 :2	1
...	..	...
1993 :4	Dln y1993 :4	1

comment capter le changement du taux de croissance d’une série

Supposons que votre série en première différence i.e. D ln y_t semble évoluer selon deux paliers différents. On aurait alors deux taux de croissance : un avant et un après! Pour estimer les deux taux de croissance, on peut effectuer la régression suivante :

D ln y_t = a₀ + a₁ + u_t

où a₀ représente le taux de croissance moyen de la première période et a₁ celui de la deuxième période.

	Variable dépendante	Variable indépendante
Période	Dln yt	Constante a0	Constante a1
1991 :2	Dln y1991 :2	1	0
...	..	...	…
1992 :3	Dln y1992 :2	1	0
1992 :4	Dln y1992 :3	0	1
…		…	…
1993 :4	Dln y1993 :4	0	1

l’écart par rapport à deux séries

Soit deux séries y_t et x_t : au lieu de transformer chaque série individuellement, on s’intéresse à la série z_t = y_t - x_t qui sera dans la plus part des cas beaucoup plus sable.

4. Saisonnalité et désaisonnalisation

Se référer à la discussion en classe.

D ln y_t = Q1 + Q2 + Q3 + Q4 + u_t

	Variable dépendante	Variables indépendantes
Période	D ln yt	Q1	Q2	Q3	Q4
1992 :1		1	0	0	0
1992 :2		0	1	0	0
1992 :3		0	0	1	0
1992 :4		0	0	0	1
...		...	...	...	...
1993 :4		0	0	0	1

Annexe : Transformation logarithmique et taux de croissance

La notion de taux de croissance est omniprésente dans l’analyse des séries chronologiques tout comme dans les calculs financiers usuels. Ainsi, on sait qu’une somme initiale A placée pendant n années à un taux R rapportera

Montant final = A(1+R)ⁿ .

De la même façon, une économie ayant un PIB initial de y₀ et qui croît à un taux g pendant t années atteindra le niveau

(1) y_t = y₀(1+g)^t.

Afin de simplifier les calculs, il est souvent préférable de procéder à la transformation suivante

(2) ln y_t = ln y₀ + ln(1+g)t

qui donne une équation linéaire, donc plus simple et estimable par les méthodes usuelles. Par exemple, on peut effectuer la régression

(3) ln y_t = a + bt

et obtenir un estimé de g en utilisant l’identité b = ln(1+g) i.e. g=e^b-1. Si les données sous-jacentes sont trimestrielles, le taux de croissance annuel est calcul de façon usuelle comme (1+g)⁴. Si les données sous-jacentes étaient annuelles, alors le taux de croissance trimestriel serait donné par (1+TauxTrimestriel)⁴=1+g.

L’équation (3) peut aussi être dérivée en faisant appel à la notion de fréquence de capitalisation. On sait une somme initiale A placée pendant n années à un taux annuel R capitalisé m fois par année rapportera

Montant final = A(1+R/m)^mn . À titre d’exemple,

R=0,1, n=1, A=100	A(1+R/m)^mn
M=1 (annuel)	110
M=2 (bi-annuel)	110,25
M=4 (trimestriel)	110,38
M=12 (mensuel)	110,47
M=52 (hebdomadaire)	110,51
M=365 (quotidien)	110.52

Une capitalisation quotidienne correspond grosso modo à une capitalisation continue où

Montant final = Ae^Rn.

De la même façon, une série qui augmente à un taux continu (ou instantané) de b peut être représentée par

(4) y_t = y₀e^bt.

En appliquant la transformation logarithmique, on obtient l’équation (3) de tout à l’heure

(5) ln y_t = a + bt

où a = ln y₀. Le coefficient b de la régression peut donc être interprété comme le taux de croissance instantané ou continu de la série y. Il s’agit là d’une simplification qui sera fort utile.

En utilisant l’approximation ln(1+x) » x, on peut monter que b = ln(1+g) » g. Par exemple, si g = 0,05, ln(1+0,05)=0,0487.

Par exemple, il arrive souvent que les chercheurs aient recours au taux de croissance d’une série. On peut bien sûr le calculer de façon usuelle à l’aide de la formule

(y_t – y_t-1)/y_t-1

i.e. le taux de croissance discret g. On peut obtenir une approximation fort utile en notant que

ln y_t = ln y₀ + bt

ln y_t-1 = ln y₀ + b(t-1) et que

ln y_t – ln y_t-1 = ln y₀ + bt – ln y₀ – b(t-1)

(6) ln y_t – ln y_t-1 = b(t-t+1) = b

La première différence du log naturel de y (ln) nous donne le taux de croissance instantané directement!

Finalement, la régression (3) ou (5) permet d’isoler la valeur ajustée de la régression (fit)

ln y_t = a*+b*t + u*_t.

ln y_t = fit_t + erreur_t.

où * indique un coefficient ou une variable estimée. Comme lny_t – lny_t-1 correspond à un taux (le taux de croissance), ln y_t - fit_t correspond aussi à un taux mais un taux différent. En fait, erreur_t peut être interprété comme la déviation en pourcentage par rapport à la tendance linéaire captée par le fit de la régression. Suite à une transformation logarithmique, la plupart des calculs ou des nombres en présence peuvent être ramenée à des unités de pourcentage. Pour vous en convaincre, l’exemple ci-dessous est fort utile.

* Transformation logarithmique

*

ALLOCATE 20

SET TREND = T

SET Y = 0

SET Y 1 20 = 1.0*EXP(.1*TREND)

SET LN_Y 1 20 = LOG(Y)

GRAPH(HEADER='Transformation logarithmique',KEY=UPLEFT) 2

# Y

# LN_Y

SET DIFF_Y 2 20 = LN_Y(T)-LN_Y(T-1)

PRINT 2 5 DIFF_Y

ENTRY DIFF_Y

2 0.1000000000000

3 0.1000000000000

4 0.1000000000000

5 0.1000000000000